Инструкция
1
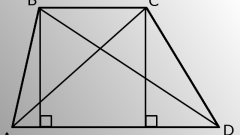
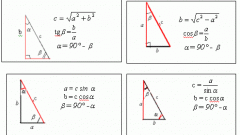
Если известны длины двух смежных сторон прямоугольника (А и В), то длину диагонали (С) определить очень просто. Исходите из того, что диагональ лежит напротив прямого угла в треугольнике, образуемом ею и этими двумя сторонами. Это позволяет применить в расчетах теорему Пифагора и вычислить длину диагонали, найдя квадратный корень из суммы возведенных в квадрат длин известных сторон: С=v(А?+В?).
2
Если известна длина лишь одной стороны прямоугольника (А), а также величина угла (?), который с ней образует диагональ, то для вычисления длины этой диагонали (С) придется использовать одну из прямых тригонометрических функций - косинус. Разделите длину известной стороны на косинус известного угла - это и будет искомая длина диагонали: С=А/cos(?).
3
Если прямоугольник задан координатами своих вершин, то задача вычисления длины его диагонали сведется к нахождению расстояния между двумя точками в этой системе координат. Примените теорему Пифагора к треугольнику, который образуют проекции диагонали на каждую из координатных осей. Допустим, прямоугольник в двухмерных координатах образован вершинами A(X?;Y?), B(X?;Y?), C(X?;Y?) и D(X?;Y?). Тогда вам нужно вычислить расстояние между точками A и C. Длина проекции этого отрезка на ось X будет равна модулю разности координат |X?-X?|, а проекции на ось Y - |Y?-Y?|. Угол между осями равен 90°, из чего вытекает, что эти две проекции являются катетами, а длина диагонали (гипотенузы) равна квадратному корню из суммы квадратов их длин: AC=v((X?-X?)?+(Y?-Y?)?).
4
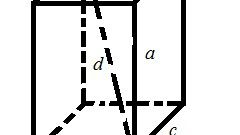
Для нахождения диагонали прямоугольника в трехмерной системе координат действуйте так же, как в предыдущем шаге, лишь добавив в формулу длину проекции на третью координатную ось: AC=v((X?-X?)?+(Y?-Y?)?+(Z?-Z?)?).
Видео по теме