Инструкция
1
В любом правильном многоугольнике углы равны между собой и вычисляются по формуле
?? = (N - 2) * 180?/N, где ?? – любой из углов правильного многоугольника, N – число вершин.
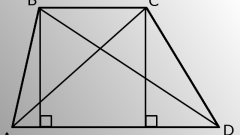
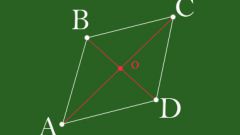
Зная углы при вершинах многоугольника, его диагонали можно вычислить, используя теорему косинусов
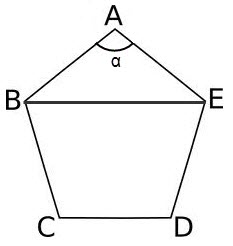
BE = v(AB? + AE? – 2 * AB * AE * cos??)
?? = (N - 2) * 180?/N, где ?? – любой из углов правильного многоугольника, N – число вершин.
Зная углы при вершинах многоугольника, его диагонали можно вычислить, используя теорему косинусов
BE = v(AB? + AE? – 2 * AB * AE * cos??)
2
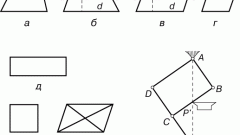
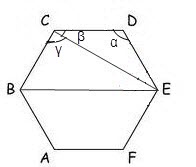
Если количество вершин больше пяти, то для вычисления диагоналей, которые соединяют вершины, лежащие на разных сторонах можно воспользоваться той же теоремой косинусов для вычисления углов образующихся треугольников. Например, в шестиугольнике ABCDEF, для нахождения диагонали BE, необходимо вычислить диагональ CE, затем по той же теореме косинусов вычислить угол ??, тогда ?? = ?? - ??. Таким образом,
BE = v(BC? + CE? – 2 * BC * CE * cos??).
BE = v(BC? + CE? – 2 * BC * CE * cos??).
Видео по теме
Обратите внимание
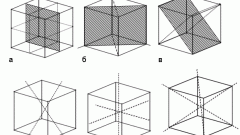
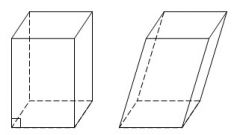
Для вычисления пространственной диагонали многогранника, необходимо построить сечение, содержащее эту диагональ, вычислить углы при вершинах этого сечения, рассматривая сечение как плоский многоугольник. Тогда диагональ можно рассчитать по приведённой выше схеме.