Инструкция
1
Понятие четырехугольник является общим названием для нескольких геометрических фигур. Это параллелограмм, прямоугольник, квадрат, ромб и трапеция. Одни из них – частные случаи других, соответственно, формулы площадей вытекают одна из другой путем различных упрощений.
2
Вычислить площадь произвольного зависимости от его разновидности. Для этого достаточно знать длины диагоналей, которых у него две, а также величину угла между ними:S = 1/2•d1•d2•sin α.
3
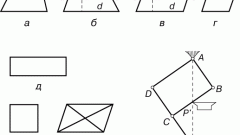
Особенность параллелограмма – попарное равенство и параллельность противолежащих сторон. Существует несколько формул для нахождения его площади: произведение стороны на высоту, проведенную к ней, а также результат умножения длин двух смежных сторон на синус угла между ними:S = a•H;S = AB•BC•sin ABC.
4
Прямоугольник, ромб, квадрат – все это частные случаи параллелограмма. У прямоугольника каждый из четырех углов составляет 90°, ромб предполагает равенство всех сторон и перпендикулярность диагоналей, а квадрат обладает свойствами их обоих, т.е. все его углы прямые, а стороны равны.
5
Исходя из этих особенностей, площади каждого из описанных фигур определяются по формулам:S_прям = a•b – сторона b является одновременно и высотой;S_ромб = 1/2•d1•d2 – следствие из общей формулы произведения диагоналей при упрощении sin 90° = 1;S_кв = a² – стороны равны и являются одновременно высотами.
6
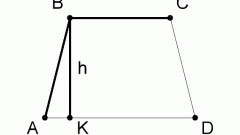
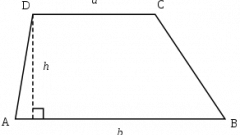
Трапеция отличается от других четырехугольников тем, что лишь две из ее противолежащих сторон параллельны. Однако они не равны между собой, а две другие стороны – не параллельны друг другу. Площадь трапеции равна произведению полусуммы оснований (параллельных сторон, обычно расположенных горизонтально) на высоту (вертикальный отрезок, соединяющий оба основания):S = (a + b)•h/2.
7
Кроме того, площадь трапеции можно вычислить, если известны все длины сторон. Это довольно громоздкая формула:S = ((a + b)/2)•√(c² - (((b - a)² + c² - d²)/(2•(b - a)))²), c и d – боковые стороны.