Инструкция
1
2
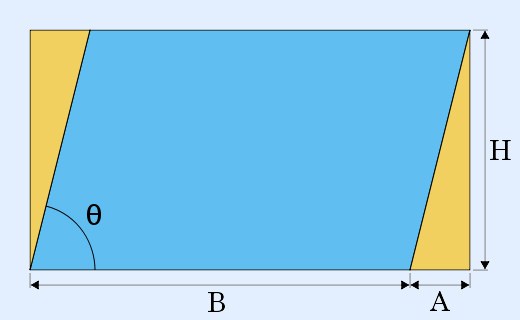
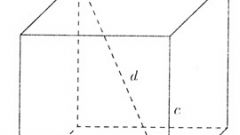
Формула нахождения площади параллелограммы выглядит следующим образом:S = a * Ha,где a – сторона;Ha – длина диагонали, проведенной к стороне a.Если неизвестна высота – вторая необходимая величина, возьмите за основу одну из сторон и проведите к ней высоту, которую предстоит найти. Поскольку образовался прямоугольный треугольник, можно применить теорему Пифагора:a = √c² – b²,b = √c² – a²c = √a² + b²где a и b – стороны прямоугольного треугольника; c – гипотенуза.
3
Ход поиска длин сторон во многом зависит от исходных данных, в некоторых случаях придется прибегнуть к тригонометрии. a = c * cos β = c * sin α = b * tg αb = c * cos α = c * sin β = a * tg βc = a /sin α = a /cos β = b /cos α = b /sin βa и b – катеты; c – гипотенуза.Для вычисления длины высоты параллелограмма с применением синусов, косинусов и тангенсов потребуется справочник по переводу их значений в число.
4
Если перед вами частный случай параллелограмма, то для поиска площади можно воспользоваться упрощенными формулами. Например, чтобы найти этот показатель по отношению к квадрату важно знать длину его стороны, которую предстоит перемножить на саму себя.S = a²,где S – площадь; a – сторона.
5
Для поиска значения площади прямоугольника подставьте значения сторон в формулу:S = a * b;где a – длина одной стороны; b – длина перпендикулярной к a стороне.
6
Еще один вариант параллелограмма – ромб. Чтобы найти значение его площади, используйте одну из формул.S = a * b /2,где a и b – длина диагоналей.S = a * Ha,где Ha – длина диагонали, проведенной к стороне a.S = a² * sin α,где α — угол между двумя смежными сторонами ромба.
Источники:
- как выглядеть четырехугольников
- Как найти площадь параллелограмма?