Вам понадобится
  • декартова, полярная и сферическая системы координат
Инструкция
1
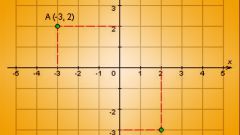
Рассмотрите для начала прямоугольную декартову систему координат. Положение точки в пространстве в этой системе координат определяется координатами x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами этой точки. Радиус-вектор точки можно также представить как диагональ прямоугольного параллелепипеда. Проекции точки на координатные оси будут совпадать с вершинами этого параллелепипеда.
2
Рассмотрите теперь полярную систему координат, в которой координата точки будет задаваться радиальной координатой r (радиус-вектор в плоскости XY), угловой координатой ? (углом между вектором r и осью X) и координатой z, аналогичной координате z в декартовой системе.
Полярные координаты точки можно перевести в декартовы следующим образом: x = r*cos?, y = r*sin?, z = z.
3
Теперь рассмотрите сферическую систему координат. В ней положение точки задается тремя координатами r, ? и ?. r - расстояние от начала координат до точки, ? и ? - азимутальные и зенитный угол соответственно. Угол ? аналогичен углу с таким же обозначением в полярной системе координат, а ? - угол между радиус-вектором r и осью Z, причем 0<= ? <= pi.
Если перевести сферические координаты в декартовы, то получится: x = r*sin?*cos?, y = r*sin?*sin?*sin?, z = r*cos?.