Инструкция
1
Выразите из любой функции аргумент x. Полученное выражение для x подставьте во вторую функцию.
2
Из получившегося уравнения найдите x. Это будут координаты точек пересечения функций. Если нет таких значений x, которые удовлетворяли бы уравнению, значит, функции не пересекаются. Если найдено единственное численное значение x, значит, функции пересекаются только в одной точке. Если же переменная x имеет несколько значений, то функции пересекаются в нескольких точках.
3
Найдите значение функции для каждой из точек пересечения (в обоих функциях эти значения должны численно совпадать, поэтому выберите ту функцию, значение которой проще найти). Вы получили полные координаты точек пересечения.
4
Запишите координаты точек пересечения в стандартном виде: (значение аргумента в точке, значение функции в точке).
5
Не забывайте про области определения функций. Может случиться так, что представленные функции не имеют общих областей определения. В таком случае, дальнейший поиск точек пересечения не имеет смысла. А может случиться так, что только одна точка является общей для областей определения функций. В таком случае, необходимо рассматривать только её одну. Например, функции "корень из x" и "корень из минус x". Обе эти функции определены лишь в точке ноль. Эта же точка будет являться и точкой пересечения функций.
Помимо этих крайних случаев, возможно еще множество вариаций. В любом случае, область определения функций следует учитывать.
6
Если необходимо найти точки пересечения функции с осью абсцисс (Ox), рассматривайте её как функцию y=0. Ось ординат (Oy) описывает уравнение x=0.
7
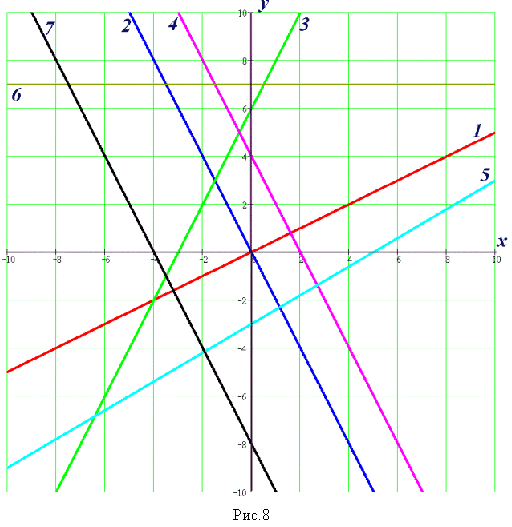
Если в задаче требуется найти точки пересечения геометрическим путем, постройте графики функций. Найдите приближенное значение координат точек, в которых эти функции пересекаются на графике. Запишите ответ.