Инструкция
1
Функция - это переменная величина, зависящая от значения аргумента. Аргумент - переменная независимая. Пределы изменений аргумента называются областью допустимых значений (ОДЗ). Поведение функции рассматривается в границах ОДЗ потому, что в этих пределах зависимость между двумя переменными не хаотическая, а подчиняется определенным правилам и может быть записана в виде математического выражения.
2
Рассмотрим произвольную функциональную зависимость F=φ(x), где φ - математическое выражение. Функция может иметь точки пересечения с осями координат или с другими функциями.
3
4
В точках пересечения функции с осью ординат значение аргумента равно нулю. Следовательно, задача превращается в нахождение значения функции при х=0. Точек пересечения функции с осью OY будет столько, сколько найдется значений заданной функции при нулевом аргументе.
5
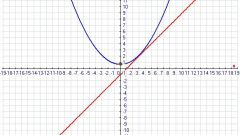
Для нахождения точек пересечения заданной функции с другой функцией необходимо решить систему уравнений:
F=φ(x)
W=ψ(x).
Здесь φ(x) — выражение, описывающее заданную функцию F, ψ(x) — выражение, описывающее функцию W, точки пересечения с которой заданной функции нужно найти. Очевидно, что в точках пересечения обе функции принимают равные значения при равных значениях аргументов. Общих точек у двух функций будет столько, сколько решений у системы уравнений на заданном участке изменений аргумента.
F=φ(x)
W=ψ(x).
Здесь φ(x) — выражение, описывающее заданную функцию F, ψ(x) — выражение, описывающее функцию W, точки пересечения с которой заданной функции нужно найти. Очевидно, что в точках пересечения обе функции принимают равные значения при равных значениях аргументов. Общих точек у двух функций будет столько, сколько решений у системы уравнений на заданном участке изменений аргумента.
Видео по теме