Инструкция
1
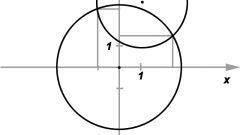
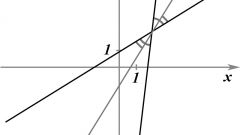
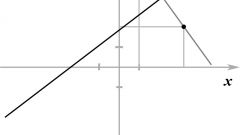
Количество возможных точек пересечения двух определенных графиков зависит от вида используемой функции. К примеру, линейные функции всегда имеют одну точку пересечения, а для квадратных характерно наличие сразу нескольких точек – двух, четырех и более. Рассмотрите этот факт на конкретном примере нахождения точки пересечения двух графиков с двумя линейными функциями. Пусть это будут функции следующего вида: y₁=k₁x+b₁ и y₂=k₂x+b₂. Для того, чтобы найти точку их пересечения, вы должны решить уравнение типа k₁x+b₁=k₂x+b₂ или y₁=y₂.
2
Преобразуйте равенство, в результате которого получится следующее: k₁x-k₂x=b₂-b₁. Затем выразите переменную х таким образом: x=(b₂-b₁)/(k₁-k₂). Теперь найдите значение х, то есть координату точки пересечения двух имеющихся графиков по оси абсцисс. Затем вычислите соответствующую координату по оси ординат. С этой целью подставьте в любую из представленных ранее функций полученное значение х. В результате вы получите координаты точки пересечения у₁ и у₂, которые будут выглядеть следующим образом: ((b₂-b₁)/(k₁-k₂);k₁(b₂-b₁)/(k₁-k₂)+b₂).
3
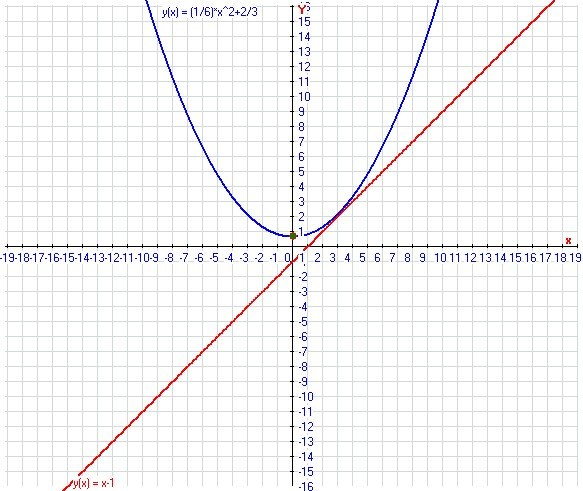
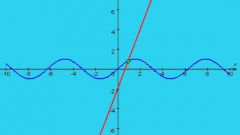
Данный пример был рассмотрен в общем виде, то есть без применения числовых значений. Для наглядности рассмотрите еще один вариант. Требуется найти точку пересечения двух графиков функций, таких как f₂ (x)=0,6x+1,2 и f₁ (x)=0,5x² . Приравняйте f₂ (x) и f₁ (x), в результате у вас должно получиться равенство следующего вида: 0,5x²=0,6x+1,2. Перенесите все имеющиеся слагаемые в левую часть, при этом у вас получится квадратное уравнение вида 0,5x² -0,6x-1,2=0. Решите это уравнение. Правильным ответом будут следующие значения: x₁≈2,26,x₂≈-1,06. Подставьте результат в любое из выражений функций. В конечном итоге вы вычислите искомые точки. В нашем примере – это т.А (2,26;2,55) и т.В (-1,06;0,56). Опираясь на рассмотренные варианты, вы всегда сможете самостоятельно найти точку пересечения двух графиков.
Видео по теме