Вам понадобится
  • треугольник, линейка, ручка, карандаш координаты вершин треугольника
Инструкция
1
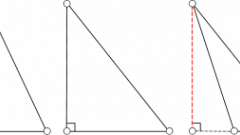
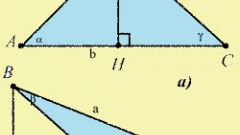
Определитесь с видом имеющегося треугольника. Самый простой случай - прямоугольный треугольник, поскольку его катеты одновременно служат и двумя высотами. Третья высота такого треугольника располагается на гипотенузе. При этом ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.
2
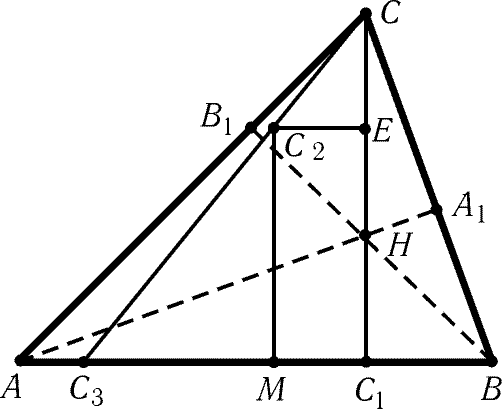
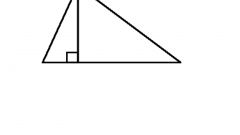
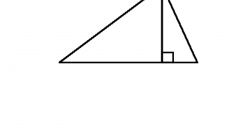
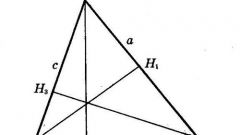
В случае остроугольного треугольника точка пересечения высот будет находиться внутри фигуры. Проведите из каждой вершины треугольника линию, перпендикулярную стороне, находящейся напротив данной вершины. Все эти линии пересекутся в одной точке. Это и будет искомый ортоцентр.
3
Точка пересечения высот тупоугольного треугольника будет находиться вне фигуры. Прежде чем проводить перпендикуляры-высоты из вершин, вам необходимо сначала продолжить линии, образующие тупой угол треугольника. Перпендикуляр в данном случае опускается не на сторону треугольника, а на линию, содержащую данную сторону. Далее опускаются высоты и находится их точка пересечения, как описано выше.
4
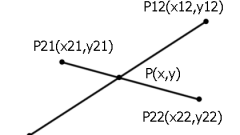
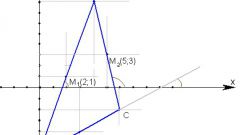
Если известны координаты вершин треугольника на плоскости или в пространстве, нетрудно найти координаты точки пересечения высот. Если А, B, C - обозначения углов, O - ортоцентра, то отрезок AО перпендикулярен отрезку BС, а BО перпендикулярен AC, таким образом, получаете уравнения AО-BC=0, BО-AC=0. Этой системы линейных уравнений достаточно для нахождения координат точки О на плоскости. Вычислите координаты векторов BC и AC, вычитая из координат второй точки соответствующие координаты первой точки. Принимаете, что точка О имеет координаты x и y (О(x,y)), далее решите систему из двух уравнений с двумя неизвестными. Если задача дана в пространстве, то в систему следует добавить уравнения AО-a=0, где вектор a=AB*AC.