Вам понадобится
  • - карандаш;
  • - линейка;
  • - циркуль.
Инструкция
1
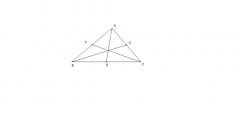
Как известно, медиана – это луч, исходящий из угла треугольника и делящий противоположную сторону пополам. В любом треугольнике их может быть до трех. Чтобы определить точку пересечения медиан треугольника, необходимо сначала выстроить эти медианы. Для этого вычертите требуемый треугольник и разделите все три его стороны строго пополам. Чтобы разделить отрезок, представляющий собой сторону треугольника, на две равные части, воспользуйтесь циркулем. Примените так называемый метод засечек.
2
Итак возьмите циркуль и поставьте его иглу в один конец отрезка-стороны. Разверните ножки циркуля на расстояние больше половины отрезка и проведите дугу таким образом, чтобы ее концы заходили за центр отрезка. Теперь переставьте ножку циркуля в противоположный конец стороны треугольника и вновь прочертите дугу – сделайте засечки. У вас по обе стороны отрезка получится по два пересечения дуг.
3
Следующим действием возьмите линейку и соедините эти точки пересечения. Линия пройдет точно через центр стороны треугольника. Проделайте то же самое с остальными двумя сторонами треугольника, то есть обозначьте их середины. Ненужные теперь нарисованные карандашные дуги можно вытереть стиральной резинкой, чтобы они не мешали дальнейшим построениям.
4
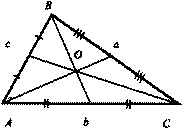
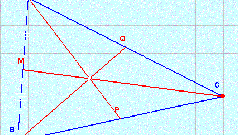
Теперь проведите медианы. Для этого возьмите снова линейку и прочертите отрезки, соединяющие отмеченные середины сторон с вершинами противоположных углов. В результате вы получите точку пересечения трех медиан треугольника.