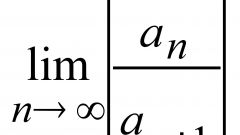Как найти медиану ряда

Для обобщенной оценки длинного ряда значений применяются различные вспомогательные методы и величины. Одной из таких величин является медиана. Хотя ее можно назвать средним значением ряда, но ее смысл и метод ее вычисления отличаются от других вариаций на тему среднего значения.

Инструкция

1. Самым распространенным способом оценить среднюю величину в ряду значений является среднее арифметическое. Чтобы его вычислить, нужно сумму всех значений ряда разделить на число этих значений. Например, если дан ряд 3, 4, 8, 12, 17, то его среднее арифметическое равно (3 + 4 + 8 + 12 + 17)/5 = 44/5 = 8,6.
2. Еще одно среднее, часто встречающееся в математических и статистических задачах, называется средним гармоническим. Среднее гармоническое от чисел a0, a1, a2… an равно n/(1/a0 + 1/a1 + 1/a2… +1/an). Например, для того же ряда, что и в предыдущем примере, среднее гармоническое будет равно 5/(1/3 + 1/4 + 1/8 + 1/12 + 1/17) = 5/(347/408) = 5,87. Среднее гармоническое всегда меньше среднего арифметического.
3. Различные средние используются в разных видах задач. Например, если известно, что автомобиль первый час ехал со скоростью A, а второй — со скоростью B, то его средняя скорость за время пути будет равна среднему арифметическому между A и B. Но если известно, что автомобиль проехал один километр со скоростью A, а следующий — со скоростью B, то, чтобы вычислить его среднюю скорость за время пути, нужно будет взять среднее гармоническое между A и B.
4. Для статистических целей среднее арифметическое представляет удобную и объективную оценку, но только в тех случаях, когда среди значений ряда нет резко выделяющихся. Например, для ряда 1, 2, 3, 4, 5, 6, 7, 8, 9, 200 среднее арифметическое будет равно 24, 5 — заметно больше всех членов ряда, кроме последнего. Очевидно, что такую оценку нельзя считать полностью адекватной.
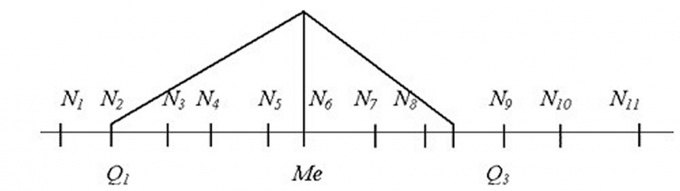
5. В таких случаях следует вычислить медиану ряда. Это средняя величина, значение которой находится ровно посередине ряда так, что все члены ряда, расположенные до медианы — не больше нее, а все, расположенные после — не меньше. Конечно, для этого нужно вначале упорядочить члены ряда по возрастанию.
6. Если в ряду a0… an нечетное количество значений, то есть n = 2k + 1, то за медиану принимается член ряда с порядковым номером k + 1. Если же количество значений четное, то есть n = 2k, то медианой считается среднее арифметическое членов ряда с номерами k и k + 1.
   Например, в уже рассмотренном ряду 1, 2, 3, 4, 5, 6, 7, 8, 9, 200 десять членов. Следовательно, его медиана — среднее арифметическое между пятым и шестым членами, то есть (5 + 6)/2 = 5,5. Эта оценка гораздо лучше отражает усредненное значение типичного члена ряда.