Вам понадобится
  • учебник по геометрии.
Инструкция
1
Стоит напомнить, что треугольник является прямоугольным, если один и его углов равен 90 градусов. А медиана - это отрезок опущенный из угла треугольника на противолежащую сторону. Причем он делит ее на две равные части. В прямоугольном треугольнике ABC, у которого угол АВС является прямым, медиана BD, опушенная из вершины прямого угла, равняется половине гипотенузы AC. То есть, для того, чтобы найти медиану, поделите значение гипотенузы на два: BD=AC/2.Пример: Пусть в прямоугольном треугольнике АВС (АВС-прямой угол), известны значения катетов AB=3 см., BC=4 см., найдите длину медианы ВD, опущенной из вершины прямого угла. Решение:
1) Найдите значение гипотенузы. По теореме Пифагора AC^2 = AB^2+BC^2. Следовательно AC = (AB^2+BC^2)^0,5 = (3^2+4^2)^0,5 = 25^0,5 = 5 см
2) Найдите длину медианы по формуле: BD = AC/2. Тогда BD = 5 см.
2
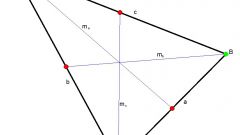
Совершенно другая ситуация возникает при нахождение медианы, опущенной на катеты прямоугольного треугольника. Пусть у треугольника АВС, угол В прямой, а АЕ и СF медианы опущенные на соответствующие катеты ВС и АВ. Тут длинна этих отрезков находится по формулам: АЕ=(2(АВ^2+AC^2)-BC^2)^0,5/2
СF=(2(BC^2+AC^2)-AB^2)^0,5/2 Пример: У треугольника АВС, угол АВС является прямым. Длина катета АВ = 8 см, угол BCA = 30 градусов. Найдите длины медиан, опущенных из острых углов.Решение:
1) Найдите длину гипотенузы АС, ее можно получить из соотношения sin(BCA)=AB/AC. Отсюда AC=AB/sin(BCA). AC=8/sin(30)=8/0,5=16 см.
2) Найдите длину катета АС. Проще всего ее можно найти по теореме Пифагора: AC = (AB^2+BC^2)^0,5, AC = (8^2+16^2)^0,5 = (64+256)^0,5 = (1024)^0,5 = 32 см.
3) Найдите медианы по выше приведенным формулам
АЕ=(2(АВ^2+AC^2)-BC^2)^0,5/2 = (2(8^2+32^2)-16^2)^0,5/2 = (2(64+1024)-256)^0,5/2 = 21,91 см.
СF=(2(BC^2+AC^2)-AB^2)^0,5/2 = (2(16^2+32^2)-8^2)^0,5/2 = (2(256+1024)-64)^0,5/2 = 24,97 см.