Вам понадобится
- Знание длин сторон треугольника.
Инструкция
1
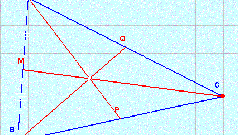
Для расчета длины медианы применяется формула (см. рис. 1), где:
mc - длина медианы;
а, b, c - стороны треугольника.
mc - длина медианы;
а, b, c - стороны треугольника.
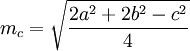
Обратите внимание
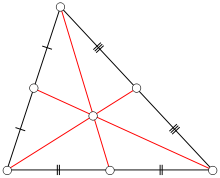
Медианы треугольника обладают свойствами:
1) любая из трех медиан разделяет исходный треугольник на два равных по площади треугольника;
2) Все медианы треугольника обладают единой точкой пересечения. Эта точка называется центром треугольника;
3) Медианы треугольника разбивают его на 6 равновеликих треугольников. Равновеликими называются геометрические фигуры с равными площадями.
1) любая из трех медиан разделяет исходный треугольник на два равных по площади треугольника;
2) Все медианы треугольника обладают единой точкой пересечения. Эта точка называется центром треугольника;
3) Медианы треугольника разбивают его на 6 равновеликих треугольников. Равновеликими называются геометрические фигуры с равными площадями.
Полезный совет
Если треугольник является равносторонним, то его медианы равны. Помимо этого, в таком треугольнике медианы совпадают с биссектрисами и высотами.
Биссектрисой называется луч, который исходит из любой вершины треугольника и делит образованный ею угол пополам.
Под высотой треугольника подразумевается отрезок, который проведен из вершины треугольника перпендикулярно противоположной стороне.
Биссектрисой называется луч, который исходит из любой вершины треугольника и делит образованный ею угол пополам.
Под высотой треугольника подразумевается отрезок, который проведен из вершины треугольника перпендикулярно противоположной стороне.