Инструкция
1
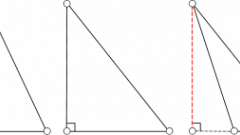
Высотой треугольника называется перпендикулярный отрезок, проведенный из какой-либо вершины на противоположную ей сторону (основание). Медиана треугольника – это отрезок, соединяющий одну из вершин с серединой противоположной стороны. Высота и медиана из одной и той же вершины могут совпадать в случае если треугольник равнобедренный, а вершина соединяет его равные стороны.
2
Задача 1Найти высоту BH и медиану BM произвольного треугольника ABC, если известно, что отрезок BH делит основание AC на отрезки с длинами 4 и 5 см, а угол ACB равен 30°.
3
РешениеФормула медианы в произвольном треугольнике представляет собой выражение ее длины через длины сторон фигуры. Из начальных данных вы знаете только одну сторону AC, которая равна сумме отрезков AH и HC, т.е. 4+5 = 9. Следовательно, целесообразно будет сначала найти высоту, затем через нее выразить недостающие длины сторон AB и BC, а потом вычислить медиану.
4
Рассмотрите треугольник BHC - он прямоугольный, исходя из определения высоты. Вам известен угол и длина одной стороны, этого достаточно для того, чтобы найти сторону BH через тригонометрическую формулу, а именно:BH = HC•tg BCH = 5/√3 ≈ 2,89.
5
Вы получили высоту треугольника ABC. По тому же принципу определите длину стороны BC:BC = HC/cos BCH = 10/√3 = 5,77.Этот результат можно проверить по теореме Пифагора, согласно которой квадрат гипотенузы равен сумме квадратов катетов:AC² = AB² + BC² → BC = √(25/3 + 25) = 10/√3.
6
Найдите оставшуюся третью сторону AB через рассмотрение прямоугольного треугольника ABH. По теореме Пифагора AB = √(25/3 + 16) = √(73/3) ≈ 4,93.
7
Запишите формулу для определения медианы треугольника:BM = 1/2•√(2•(AB² + BC²) – AC²) = 1/2•√(2•(24,3 + 33,29) – 81) ≈ 2,92.Оформите ответ задачи: высота треугольника BH = 2,89; медиана BM = 2,92.
Видео по теме