Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы пересекаются в одной точке всегда внутри треугольника. Эта точка делит каждую медиану в отношении 2:1.
Медиану можно найти используя теорему Стюарта. Согласно которой, квадрат медианы равен четверти суммы удвоенных квадратов сторон минус квадрат стороны, к которой проведена медиана. mc^2 = (2a^2 + 2b^2 - c^2)/4, где a, b, c - стороны треугольника. mc - медиана к стороне с;
2
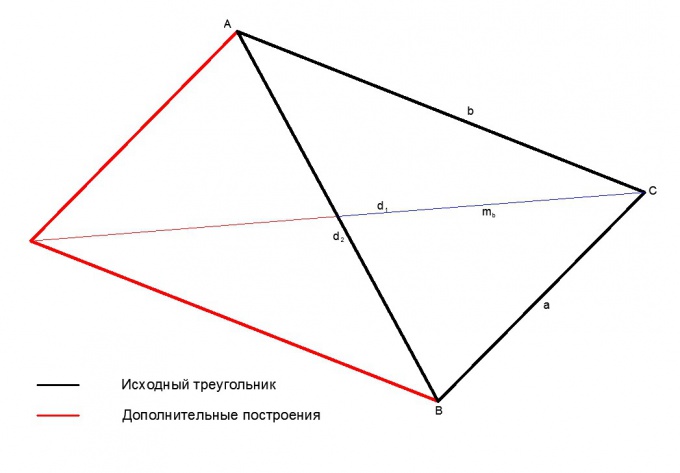
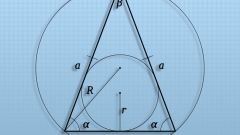
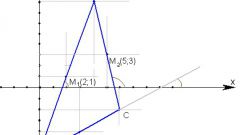
Задача по нахождению медианы может быть решена через дополнительные построения треугольника до параллелограмма и решение через теорему о диагоналях параллелограмма.Продлим стороны треугольника и медиану, достроив их до параллелограмма. Таким образом, медиана треугольника будет равна половине диагонали получившегося параллелограмма, две стороны треугольника - его боковым сторонам (a, b), а третья сторона треугольника, к которой была проведена медиана, является второй диагональю получившегося параллелограмма. Согласно теореме, сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон. 2*(a^2 + b^2) = d1^2 + d2^2, где d1, d2 - диагонали получившегося параллелограмма; отсюда: d1 = 0.5*v(2*(a^2 + b^2) - d2^2)
