Вам понадобится
- Инструменты: Карандаш Линейка Транспортир Математические формулы и понятия: Медиана Теоремы синусов и косинусов
Инструкция
1
Постройте треугольник с заданными параметрами - по трем сторонам, по двум сторонам и углу между ними, по двум углам и расположенной между ними стороне.
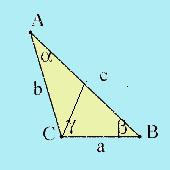
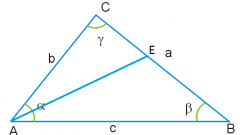
Обозначьте вершины углов, углы и стороны. Вершины углов обозначаются А, B, C, сами углы - греческими символами ?,?,?. Стороны обозначаются строчными латинскими буквами a,b,c.
Вычислите длины всех углов и сторон по теоремам синусов и косинусов.
Обозначьте вершины углов, углы и стороны. Вершины углов обозначаются А, B, C, сами углы - греческими символами ?,?,?. Стороны обозначаются строчными латинскими буквами a,b,c.
Вычислите длины всех углов и сторон по теоремам синусов и косинусов.
2
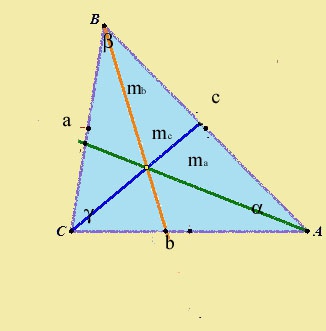
Вспомните, что такое медиана. Медиана - это линия, проведенная из заданного угла треугольника к середине его противолежашей стороны.
Разделите стороны треугольника пополам и обозначьте получившиеся точки латинской M с соответствующими сторонам нижниими индексами a,b,c.
Разделите стороны треугольника пополам и обозначьте получившиеся точки латинской M с соответствующими сторонам нижниими индексами a,b,c.
3
Вычислите длину медианы по формуле: медиана равна квадратному корню из суммы удвоенных квадратов двух других сторон треугольника минус квадрат стороны, к которой проведена медиана, деленному на четыре.
Вычислите по этой же формуле размеры остальных медиан
Вычислите по этой же формуле размеры остальных медиан
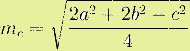
Видео по теме
Обратите внимание
Все медианы треугольника пересекаются в одной точке. Эта точка называется центроидом. Самой длинной стороне треугольника соответствует самая короткая медиана. В прямоугольном треугольнике медиана, проведенная из прямого угла, является одновременно высотой к этой же стороне.
Полезный совет
Для определения синусов и косинусов пользуйтеся математическими таблицами.
Источники:
- пїЅпїЅпїЅ пїЅпїЅпїЅпїЅпїЅ, пїЅпїЅпїЅпїЅпїЅ найти длину медианы