Инструкция
1
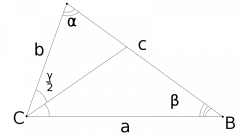
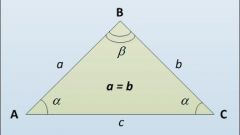
Если вам известны длины сторон (a и b) треугольника, образующие разделенный пополам угол (γ), то длину биссектрисы (L) можно вывести из теоремы косинусов. Для этого найдите значение удвоенного произведения длин сторон на косинус половины угла между ними и разделите полученный результат на сумму длин сторон: L=2*a*b*cos(γ/2)/(a+b).
2
Если величина угла, который делится биссектрисой, неизвестна, но даны длины всех сторон треугольника (a, b и c), то для вычислений удобнее ввести дополнительную переменную - полупериметр: p=½*(a+b+c). После этого часть формулы длины биссектрисы (L) из предыдущего шага надо будет заменить - в числитель дроби поставьте удвоенный квадратный корень из произведения длин сторон, образующих разделенный биссектрисой угол, на полупериметр и частное от вычитания из полупериметра длины третьей стороны. Знаменатель же оставьте без изменений - это должна быть сумма длин сторон разделенного угла треугольника. В результате формула должна выглядеть так: L=2*√(a*b*p*(p-c))/(a+b).
3
Если усложнить подкоренное выражение формулы из предыдущего шага, то можно обойтись и без полупериметра. Для этого оставьте знаменатель (сумма длин сторон разделенного угла) без изменений, а в числителе должен быть квадратный корень из произведения длин этих же сторон на сумму их длин, из которой вычтена длина третьей стороны, а также на сумму длин всех трех сторон: L=√(a*b*(a+b-c)*(a+b+c))/(a+b).
4
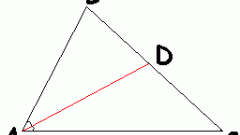
Если в исходных условиях даны не только длины сторон (a и b), образующих разделенный биссектрисой угол, но и длины отрезков (d и e), на которые эта биссектриса поделила третью сторону, то тоже придется извлекать квадратный корень. Длину биссектрисы (L) в этом случае рассчитывайте как корень из произведения длин известных сторон, из которого вычтено произведение длин отрезков: L=√(a*b-d*e).