Вам понадобится
- - тетрадь;
- - карандаш;
- - линейка.
Инструкция
1
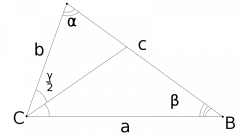
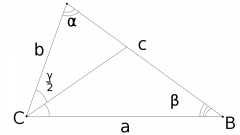
Доказать теорему невозможно без знания ее составляющих и их свойств. Важно обратить внимание на то, что биссектриса угла, в соответствии с общепринятым понятием, представляет собой луч, выходящий из вершины угла и делящий его на еще два равных угла. При этом биссектриса угла считается особым геометрическим местом расположения точек внутри угла, которые равноудалены от его сторон. Согласно выдвигаемой теореме, биссектриса угла также представляет собой отрезок, выходящий из угла и пересекающийся с противоположной стороной треугольника. Данное утверждение и следует доказать.
2
Ознакомьтесь с понятием отрезка. В геометрии это часть прямой, ограниченная двумя или более точками. Учитывая, что точка в геометрии является абстрактным объектом без каких-либо характеристик, можно сказать, что отрезок – расстояние между двумя точками, например, A и B. Точки, ограничивающие отрезок, называются его концами, а расстояние между ними - его длиной.
3
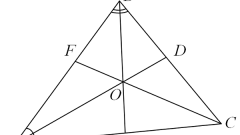
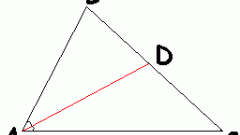
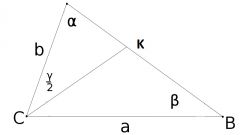
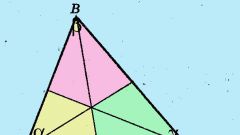
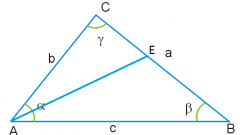
Приступите к доказательству теоремы. Сформулируйте ее подробное условие. Для этого можно рассмотреть треугольник АВС с биссектрисой BK, выходящей из угла В. Докажите, что BK является отрезком. Через вершину С проведите прямую СМ, которая будет проходить параллельно биссектрисе ВК до пересечения со стороной АВ в точке М (для этого сторону треугольника нужно продолжить). Поскольку ВК является биссектрисой угла АВС, значит, углы АВК и КВС равны между собой. Также равными будут являться углы АВК и ВМС потому, что это соответственные углы двух параллельных прямых. Следующий факт заключается в равенстве углов КВС и ВСМ: это углы, лежащие накрест при параллельных прямых. Таким образом, угол ВСМ равен углу ВМС, и треугольник ВМС является равнобедренным, поэтому ВС=ВМ. Руководствуясь теоремой о параллельных прямых, которые пересекают стороны угла, вы получите равенство: АК/КС=АВ/ВМ=АВ/ВС. Таким образом, биссектриса внутреннего угла делит противоположную сторону треугольника на пропорциональные его прилежащим сторонам части и является отрезком, что и требовалось доказать.
Видео по теме