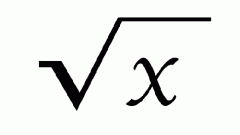Инструкция
1
Любое квадратное уравнение имеет вид: ax^2 + bx + c = 0, где x^2 – икс в квадрате, a, b, c – произвольные множители (могут иметь знак «плюс» или «минус»), х – корень уравнения. А дискриминант – корень квадратный из выражения: /b^2 – 4 * a * c /, где b^2- b во второй степени. Таким образом, чтобы вычислить корень из дискриминанта, нужно подставить множители из уравнения в выражение дискриминанта. Для этого запишите с столбик данное уравнение и его общий вид, чтобы стало видно соответствие между членами.Пример. Дано уравнение 5х + 4х^2 + 1 = 0, где х^2 – икс в квадрате. Его правильная запись выглядит так: 4х^2 + 5х + 1 = 0, а общий вид ax^2 + bx + c = 0. Отсюда видно, что множители соответственно равны: a = 4 , b = 5, c = 1.
2
Далее выбранные множители подставьте в уравнение дискриминанта.Пример. Общий вид формулы дискриминанта корень квадратный из выражения: /b^2 – 4 * a * c/, где b^2- b во второй степени (см. в рисунке). Из предыдущего шага известно, что a = 4 , b = 5, c = 1. Тогда, дискриминант равен корень квадратный из выражения: /5^2 – 4 * 4 * 1/, где 5^2- пять во второй степени.
3
Вычислите числовое значение, это и есть корень дискриминанта.
Пример. Корень квадратный из выражения: /5^2 – 4 * 4 * 1 /, где 5^2- пять во второй степени равен корню квадратному из девяти. А корень из «9» равен 3.
Пример. Корень квадратный из выражения: /5^2 – 4 * 4 * 1 /, где 5^2- пять во второй степени равен корню квадратному из девяти. А корень из «9» равен 3.
4
Вследствие того, что множители могут иметь любой знак, в уравнении могут меняться знаки. Вычисляйте такие задачи, учитывая правила сложения и вычитания чисел с разными знаками. Пример. -7х^2 + 4х + 3=0. Дискриминант равен корню из выражения: /b^2 – 4 * a * c/, где b^2- b во второй степени, тогда он имеет числовое выражение: 4^2 – 4 * (-7) * 3 = 100. А корень из «ста» равен десяти.
Видео по теме
Обратите внимание
Если подкоренное выражение дискриминанта имеет отрицательное значение. То его вычислять нельзя. Такое уравнение не имеет решений.
Полезный совет
Если корень из дискриминанта равен нулю, то данное квадратное уравнение имеет один корень.
Источники:
- формула корней дискриминанта