Инструкция
1
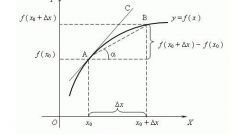
Метод дифференцирования применяется для нахождения функции, производной от исходной. Производная функция — это отношение предела приращения функции к приращению аргумента. Это самое распространенное представление производной, которую принято обозначать знаком апострофа «’». Возможно неоднократное дифференцирование функции, при этом образуются первая производная f’(x), вторая f’’(x) и т.д. Производные высших порядков обозначают f^(n)(x).
2
Чтобы продифференцировать функцию, можно воспользоваться формулой Лейбница:(f*g)^(n) = Σ C(n)^k*f^(n-k)*g^k, где C(n)^k– принятые биномиальные коэффициенты. Простейший случай первой производной легче рассмотреть на конкретном примере: f(x) = x^3.
3
Итак, по определению:f’(x) = lim ((f(x) – f(x_0))/(x – x_0)) = lim ((x^3 – x_0^3)/(x – x_0)) = lim ((x – x_0)*(x^2 +x* x_0 + x_0^2)/(x – x_0)) = lim (x^2 + x*x_0 + x_0^2) при x, стремящемся к значению x_0.
4
Избавляемся от знака предела, подставляя в полученное выражение значение x, равное x_0. Получаем:f’(x) = x_0^2 + x_0*x_0 + x_0^2 = 3*x_0^2.
5
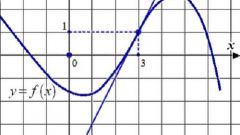
Рассмотрим дифференцирование сложных функций. Такими функциями являются композициями или суперпозициями функций, т.е. результат одной функции является аргументом для другой:f = f(g(x)).
6
Производная такой функции имеет вид:f’(g(x)) = f’(g(x))*g’(x), т.е. равна произведению старшей функции по аргументу младшей на производную младшей функции.
7
Чтобы продифференцировать композицию из трех и более функций, применяют то же правило по следующему принципу:f’(g(h(x))) = f’(g(h(x)))*(g(h(x)))’ = f’(g(h(x)))*g’(h(x))*h’(x).
8
Знание производных некоторых простейших функций является хорошим подспорьем в решении задач на дифференциальное исчисление:- производная константы равна 0;- производная простейшей функции аргумента в первой степени x’ = 1;- производная суммы функций равна сумме их производных: (f(x) + g(x))’ = f’(x) + g’(x);- аналогично производная произведения равна произведению производных;- производная частного двух функций: (f(x)/g(x))’ = (f’(x)*g(x) – f(x)*g’(x))/g^2(x);- (C*f(x))’ = C*f’(x), где C – константа;- при дифференцировании степень одночлена выносится в виде множителя, а сама степень понижается на 1: (x^a)’ = a*x^(a-1);- тригонометрические функции sinx и cosx в дифференциальном исчислении носят соответственно нечетный и четный характер - (sinx)’ = cosx и (cosx)’ = - sinx;- (tg x)’ = 1/cos^2 x;- (ctg x)’ = - 1/sin^2 x.