Вам понадобится
  • лист бумаги, функция, ручка
Инструкция
1
Для того чтобы определить чётную функцию, прежде всего запомните её определение. Функцию f (x) можно назвать чётной, если для любого значения х (икс) из области определения выполняются оба равенства: а) -x € D;
б) f (-x) = f (x).
2
Запомните, что если при противоположных значениях x (икс) значения y (игрек) равны, то исследуемая функция является чётной.
3
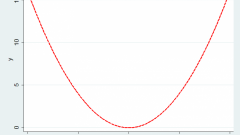
Рассмотрите пример чётной функции. Y = x?. В этом случае при значении x = -3, y = 9, и при противоположном значении x = 3 y = 9. Обратите внимание, данный пример доказывает, что при противоположных значениях x (икс) (3 и -3) значения y (игрек) равны.
4
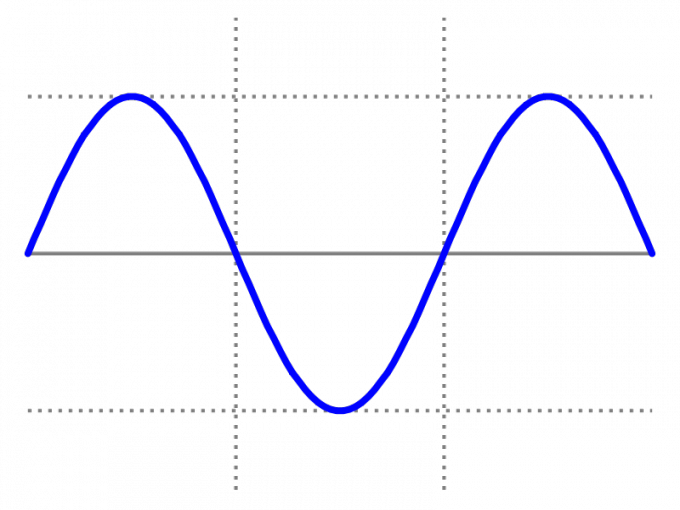
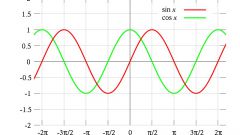
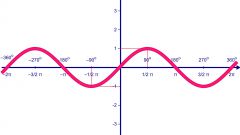
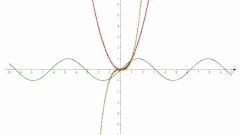
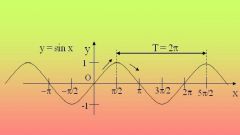
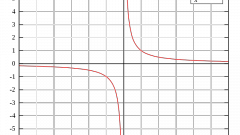
Обратите внимание, что на всей области определения график чётной функции симметричен оси OY, в то время как график нечётной функции на все области определения симметричен относительно начала координат. Простейшим примером чётной функции служат функции y = cos x; y = ?x?; y = x? + ?x?.
5
Если точка (a; b) принадлежит графику чётной функции, то и симметричная ей относительно оси ординат точка
(-a; b) также принадлежит данному графику, из чего следует, что график чётной функции симметричен относительно оси ординат.
6
Помните, что не каждая функция обязательно является либо чётной, либо нечётной. Некоторые из функций могут быть суммой чётной и нечётной функций (примером может служить функция f (x) = 0).
7
При исследований функции на чётность, запомните и оперируйте следующими утверждениями: а) сумма чётных (нечётных) функций также является чётной (нечётной) функцией; б) произведение двух чётных или нечётных фунций является чётной функцией; в) произведение нечётной и чётной функций является нечётной функцией; г) если функция f чётна (либо нечётна), то и функция 1/f также является чётной (либо нечётной).
8
Функция называется чётной, если при изменении знака аргумента значение функции остаётся неизменным. f (x) = f (-x). Используйте этот простой способ для определения чётности функции: если значение останется неизменным при умножении на -1, то функция – чётная.