Как найти угол между касательными

Прямая линия, имеющая с окружностью одну общую точку, является касательной к окружности. Другая особенность касательной – она всегда перпендикулярна радиусу, проведенному в точку касания, то есть касательная и радиус образуют прямой угол. Если из одной точки А проведены две касательных к окружности АВ и АС, то они всегда равны между собой. Определение угла между касательными (угол АВС) производится с помощью теоремы Пифагора.

Инструкция

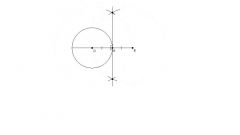
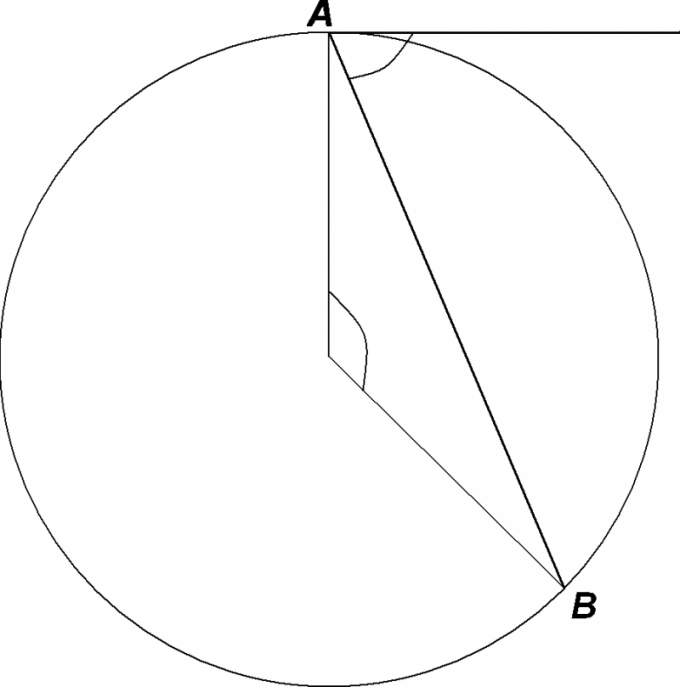
1. Для определения угла необходимо знать радиус окружности ОВ и ОС и расстояние точки начала касательной от центра окружности - О. Итак, углы АВО и АСО равны 90 градусов, радиус ОВ, например 10 см, а расстояние до центра окружности АО равно 15 см. Определите длину касательной по формуле в соответствии с теоремой Пифагора: АВ = квадратный корень из АО2 – ОВ2 или 152 - 102 = 225 – 100 = 125;
   
2. Извлеките квадратный корень. Получится 11.18 см. Поскольку угол ВАО представляет собой sin или отношение сторон ВО и АО вычислите его значение: Sin угла ВАО = 10 : 15 = 0.66
3. Затем, пользуясь таблицей синусов, найдите данное значение, которое соответствует примерно 42 градусам. Таблица синусов используется для решения различных задач – физических, математических или инженерных. Остается выяснить величину угла ВАС, для чего следует величину данного угла удвоить, то есть, получится примерно 84 градусов.
4. Величина центрального угла соответствует угловой величине дуги, на которую он опирается. Величину угла можно также определить с помощью транспортира, приложив его к чертежу. Так как подобные вычисления относятся к тригонометрии, то можно воспользоваться тригонометрическим кругом. С его помощью можно переводить градусы в радианы и наоборот.
5. Как известно, полный круг составляет 360 градусов или 2П радиан. На тригонометрическом круге отображены значения синусов и косинусов основных углов. Стоит напомнить, что значение синуса находится на оси Y, а косинуса на оси Х. Значения синуса и косинуса находятся в промежутке от -1 до 1.
6. Определить значения тангенса и котангенса угла можно поделив синус на косинус, а котангенса наоборот – косинуса на синус. Тригонометрический круг позволяет определить знаки всех тригонометрических функций. Так, синус - это нечетная функция, а косинус – четная. Тригонометрический круг позволяет понять, что синус и косинус – периодические функции. Как известно, период равен 2П.