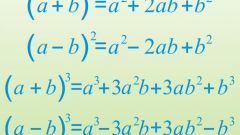Инструкция
1
Вынесение общего множителя за скобки – один из самых распространенных способов разложения на множители. Этот прием применяется для упрощения структуры длинных алгебраических выражений, т.е. многочленов. Общим множителем может быть число, одночлен или двучлен, а для его поиска применяется распределительное свойство умножения.
2
Число.Посмотрите внимательно на коэффициенты при каждом элементе многочлена, можно ли разделить их на одно и то же число. Например, в выражении 12•z³ + 16•z² – 4 очевидным является множитель 4. После преобразования получится 4•(3•z³ + 4•z² - 1). Иными словами, это число является наименьшим общим целочисленным делителем всех коэффициентов.
3
Одночлен.Определите, входит ли одна и та же переменная в каждый из слагаемых многочлена. Предположим, что это так, теперь посмотрите на коэффициенты, как в предыдущем случае. Пример: 9•z^4 – 6•z³ + 15•z² – 3•z.
4
Каждый элемент этого многочлена содержит переменную z. Кроме того, все коэффициенты – числа, кратные 3. Следовательно, общим множителем будет одночлен 3•z:3•z•(3•z³ – 2•z² + 5•z - 1).
5
Двучлен.За скобки выносится общий множитель из двух элементов, переменной и числа, которое является решением общего многочлена. Поэтому, если множитель-двучлен неочевиден, то нужно найти хотя бы один корень. Выделите свободный член многочлена, это коэффициент без переменной. Теперь примените метод подстановки в общее выражение всех целочисленных делителей свободного члена.
6
Рассмотрите пример: z^4 – 2•z³ + z² - 4•z + 4. Проверьте, не является ли какой-либо из целых делителей числа 4 корнем уравнения z^4 – 2•z³ + z² - 4•z + 4 = 0. Путем простой подстановки найдите z1 = 1 и z2 = 2, значит, за скобки можно вынести двучлены (z - 1) и (z - 2). Для того, чтобы найти оставшееся выражение, воспользуйтесь последовательным делением в столбик.

7
Запишите результат (z - 1)•(z - 2)•(z² + z + 2).