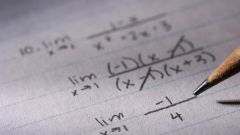Инструкция
1
Наиболее распространенным методом решения уравнений высших степеней является разложение на множители. Этот подход представляет собой комбинацию подбора целочисленных корней, делителей свободного члена, и последующее деление общего многочлена на двучлен вида (x – x0).
2
Например, решите уравнение x^4 + x³ + 2·x² – x – 3 = 0.Решение.Свободным членом данного многочлена является -3, следовательно, его целочисленными делителями могут быть числа ±1 и ±3. Подставьте их по очереди в уравнение и выясните, получится ли тождество:1: 1 + 1 + 2 – 1 – 3 = 0.
3
Итак, первый же предположительный корень дал правильный результат. Разделите многочлен уравнения на (x - 1). Деление многочленов выполняется столбиком и отличается от обычного деления чисел только наличием переменной.
4
Перепишите уравнение в новом виде (x - 1)·(x³ +2·x² + 4·x + 3) = 0. Наибольшая степень многочлена уменьшилась до третьей. Продолжите подбор корней уже для кубического многочлена:1: 1 + 2 + 4 + 3 ≠ 0;-1: -1 + 2 – 4 + 3 = 0.
5
Второй корень x = -1. Поделите кубический многочлен на выражение (x + 1). Запишите получившееся уравнение (x - 1)·(x + 1)·(x² + x + 3) = 0. Степень понизилась до второй, следовательно, уравнение может иметь еще два корня. Чтобы найти их, решите квадратное уравнение:x² + x + 3 = 0D = 1 – 12 = -11
6
Дискриминант – отрицательная величина, значит, действительных корней у уравнения больше нет. Найдите комплексные корни уравнения:x = (-2 + i·√11)/2 и x = (-2 – i·√11)/2.
7
Запишите ответ:x1,2 = ±1; x3,4 = -1/2 ± i·√11/2.
8
Другой метод решения уравнения высшей степени – замена переменных для приведения его к квадратному. Такой подход используется, когда все степени уравнения четные, например:x^4 – 13·x² + 36 = 0
9
Это уравнение называется биквадратным. Чтобы привести его к квадратному, сделайте замену y = x². Тогда:y² – 13·y + 36 = 0D = 169 – 4·36 = 25y1 = (13 + 5)/2 = 9; y2 = (13 - 5)/2 = 4.
10
Теперь найдите корни исходного уравнения:x1 = √9 = ±3; x2 = √4 = ±2.
