Под неполным квадратным уравнением понимается квадратное уравнение нестандартного вида, в котором отсутствует один из членов - b или c. При этом для решения данное уравнение необходимо привести к полному виду и правильно выстроить. При варианте аz² + с = 0 в уравнении второй член b=0, а в уравнении аz² + bz = 0 третий член с=0. Причем первый член а должен обязательно быть отличным от нуля. Решение неполного квадратного уравнения находится классическим методом через дискриминант после приведения к полному виду. Однако в каждом из частных случаев уравнения легче найти корни другим способом.
Приведите заданное неполное квадратное уравнение к полному виду: аz² + bz + c = 0. Для этого определите, какой из множителей равен нулю. Далее можно решать обычное квадратное уравнение с помощью нахождения дискриминанта и корней.
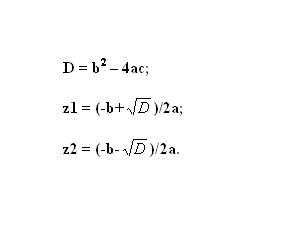
2
Если задано неполное уравнение вида аz² + bz = 0, его корни можно определить более простым способом. Для этого вынесите z за скобки. Вы получите запись: z(аz + b) = 0. Множители можно расписать: z=0 и аz + b = 0, так как оба выражения могут при умножении давать в результате ноль. В записи аz + b = 0 перенесем второй множитель вправо с другим знаком. Отсюда получаем решения z1 = 0 и z2 = -b/а. Это и есть корни исходного уравнения.
3
Если же имеется неполное уравнение вида аz² + с = 0, в данном случае решение находятся простым переносом свободного члена в правую часть уравнения. Также поменяйте при этом его знак. Получится запись аz² = -с. Выразите z² = -с/а. Возьмите корень и запишите два решения - положительное и отрицательное значение корня квадратного.
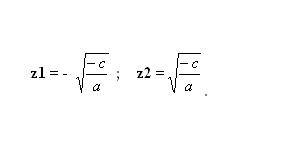
Обратите внимание
При наличии в уравнении дробных коэффициентов помножьте все уравнение на соответствующий множитель так, чтобы избавиться от дробей.
