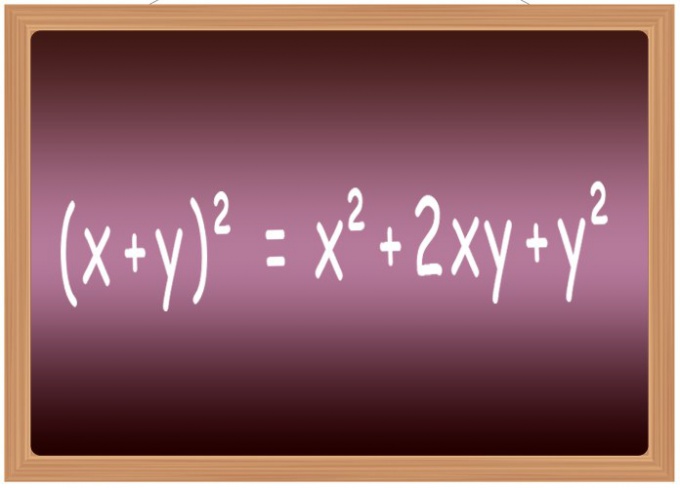Инструкция
1
Умножьте уравнение на само себя - это и есть операция возведения во вторую степень, то есть в квадрат. Если исходное выражение содержит переменные в какой-либо степени, то показатель степени следует увеличить в два раза. Например, (4*x³)² = (4*x³)*(4*x³) = 16*x⁶. Если присутствующие в уравнении численные коэффициенты умножить в уме не представляется возможным, то используйте калькулятор, онлайн-вычислитель или сделайте это на бумаге, «в столбик».
2
Если исходное выражение содержит несколько складываемых или вычитаемых переменных с численными коэффициентами (то есть является многочленом), то придется осуществлять операцию умножения по соответствующим правилам. Это означает, что следует перемножить каждый член уравнения-множимого на каждый член уравнения-множителя, а затем упростить полученное выражение. Тот факт, что в вашем случае оба уравнения одинаковы, ничего не меняет в этом правиле. Например, если возвести в квадрат требуется уравнение x²+4-3*x, то всю операцию можно записать в таком виде: (x²+4-3*x)² = (x²+4-3*x)*(x²+4-3*x) = x⁴+4*x²-3*x³ + 4*x²+16-12*x - 3*x³-12*x+9*x². Полученное выражение следует упростить и, если это возможно, расположить степенные члены в порядке убывания показателя степени: x⁴+4*x²-3*x³ + 4*x²+16-12*x - 3*x³-12*x+9*x² = x⁴ - 6*x³ + 25*x² - 24*x + 16.
3
Формулы возведения в квадрат некоторых наиболее часто встречающихся выражений лучше запомнить наизусть. В школе их обычно включают в список, называемый «формулами сокращенного умножения». В него относят, в частности, формулы возведения во вторую степень суммы двух переменных (x+y)² = x²+2*x*y+y², их разности (x-y)² = x²-2*x*y+y², суммы трех слагаемых (x+y+z)² = x²+y²+z²+2*x*y+2*y*z+2*x*z и разности трех слагаемых (x-y-z)² = x²+y²+z²-2*x*y+2*x*y-2*z.
Видео по теме