Для решения кубических уравнений разработано несколько математических методов. Часто используется метод подстановки или замены куба вспомогательной переменной, а также ряд итерационных методов, в частности, метод Ньютона. Но классическое решение кубического уравнения выражается в применении формул Виета и Кардано. Метод Виета-Кардано основан на использовании формулы куба суммы коэффициентов и применим для любого вида кубического уравнения. Для поиска корней уравнения его запись необходимо представить в виде: x³+a*x²+b*x+c=0, где a - не нулевое число.
Запишите исходное кубическое уравнение в виде: x³+a*x²+b*x+c=0. Для этого все коэффициенты уравнения поделите на первый коэффициент при множителе x³, так чтобы он стал равен единице.
2
Исходя из алгоритма метода Виета-Кардано, вычислите значения R и Q по соответствующим формулам: Q =(a²-3b)/9, R=(2a³-9ab+27c)/54. Причем коэффициенты a, b и с являются коэффициентами приведенного уравнения.
3
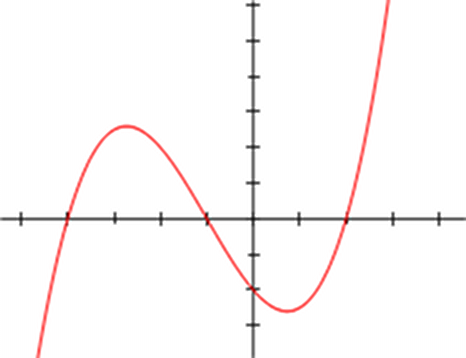
Сравните полученные значения R и Q. Если верновыражение Q³ >R² , следовательно, в исходном уравнении присутствуют 3 действительных корня. Вычислите их по формулам Виета.
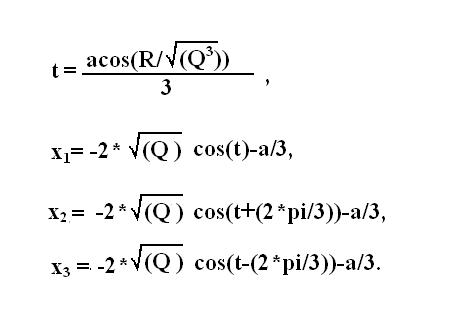
4
При значениях Q³ <= R² , в решении находится один действительный корень х1 и два комплексно-сопряженных корня. Для их определения нужно найти промежуточные значения А и В. Вычислите их по формулам Кардано.
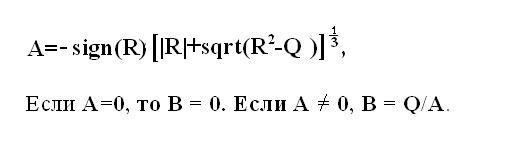
5
Найдите первый действительный корень по формуле x1=(B + A) - a/3. При различных значениях А и В определите комплексно-сопряженных корни кубического уравнения по соответствующим формулам.
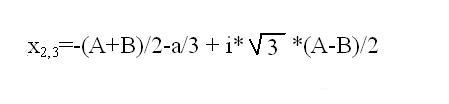
6
Если значения А и В получились равными, то сопряженные корни вырождаются во второй действительный корень исходного уравнения. Это тот случай, когда действительных корня получается два. Вычислите второй действительный корень по формуле x2=-A-a/3.
