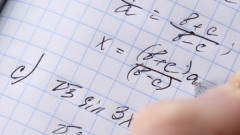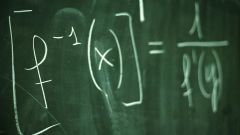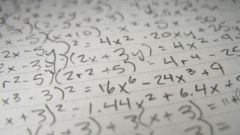Инструкция
1
Алгебраическое уравнение второй степени называется квадратным. Классическая форма левой стороны этого уравнения представляет собой многочлен a•x² + b•x + c. Чтобы вывести формулу для решения, необходимо выделить из трехчлена квадрат двучлена. Это можно осуществить двумя способами. Перенесите свободный член с в правую сторону со знаком минус:a•x² + b•x = -c.
2
Умножьте обе стороны уравнения на 4•а:4•a²•x² + 4•a•b•x = -4•a•c.
3
Прибавьте выражение b²:4•a²•x² + 4•a•b•x + b² = -4•a•c + b².
4
Очевидно, что слева получилась развернутая форма квадрата двучлена, состоящего из слагаемых 2•a•x и b. Сверните этот трехчлен в полный квадрат:(2•a•x + b)² = b² – 4•a•c → 2•a•x + b = ±√(b² – 4•a•c)
5
Откуда:x1,2 = (-b ± √(b² – 4•a•c))/2•a.Разность, стоящая под знаком корня, называется дискриминантом, а формула является общеизвестной для решения подобных уравнений.
6
Второй способ подразумевает выделение из одночлена первой степени удвоенного произведения элементов. Т.е. необходимо определить из слагаемого вида b•x, какие множители могут быть использованы для полного квадрата. Этот метод лучше рассмотреть на примере:x² + 4•x + 13 = 0
7
Посмотрите на одночлен 4•x. Очевидно, что его можно представить в виде 2•(2•x), т.е. удвоенного произведения х и 2. Следовательно, выделять нужно квадрат суммы (х + 2). Для полноты картины не хватает слагаемого 4, которое можно взять из свободного члена:x² + 4•x + 4 - 9 → (x + 2)² = 9
8
Извлеките квадратный корень:x + 2 = ±3 → x1 = 1; x2 = -5.
9
Метод выделения квадрата двучлена широко применяется для упрощения громоздких алгебраических выражений наряду с другими способами: группировка, замена переменной, вынесение общего множителя за скобку и т.д. Полный квадрат является одной из формул сокращенного умножения и частным случаем Бинома Ньютона.