Как решать степени

Уравнения высшей степени - это уравнения, в которых старшая степень переменной больше 3. Существует общая схема для решения уравнений высших степеней с целыми коэффициентами.

Инструкция

1. Очевидно, что если коэффициент при старшей степени переменной не равен 1, то можно разделить все члены уравнения на этот коэффициент и получить приведенное уравнение, поэтому сразу рассматривают приведенное уравнение. Общий вид уравнения высшей степени представлен на рисунке.
   
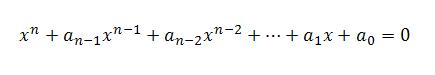
2. Первым делом находят целые корни уравнения. Целые корни уравнения высшей степени являются делителями a0 - свободного члена. Для их нахождения раскладывают a0 на множители (необязательно простые) и поочередно проверяют, какие из них являются корнями уравнения.
3. Когда находят среди делителей свободного члена такое x1, которое обращает многочлен в ноль, то можно представить исходный многочлен в виде произведения одночлена и многочлена степени n-1. Для этого исходный многочлен делят на x - x1 в столбик. Теперь общий вид уравнения изменился.
   
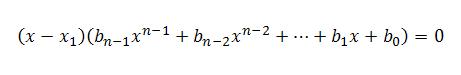
4. Далее продолжают подставлять делители a0, но уже в получившееся уравнение меньшей степени. Причем начинают с x1, так как у уравнения высшей степени могут быть кратные корни. Если находятся еще корни, то снова делят многочлен на соответствующие одночлены. Таким образом раскладывают многочлен так, чтобы получить в итоге произведение одночленов и многочлен степени 2, 3 или 4.
   
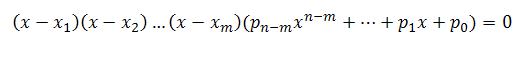
5. Находят корни многочлена младшей степени, пользуясь известными алгоритмами. Это нахождение дискриминанта для квадратного уравнения, формула Кардано для кубического уравнения и всевозможные замены,
   преобразования и формула Феррари для уравнений четвертой степени.