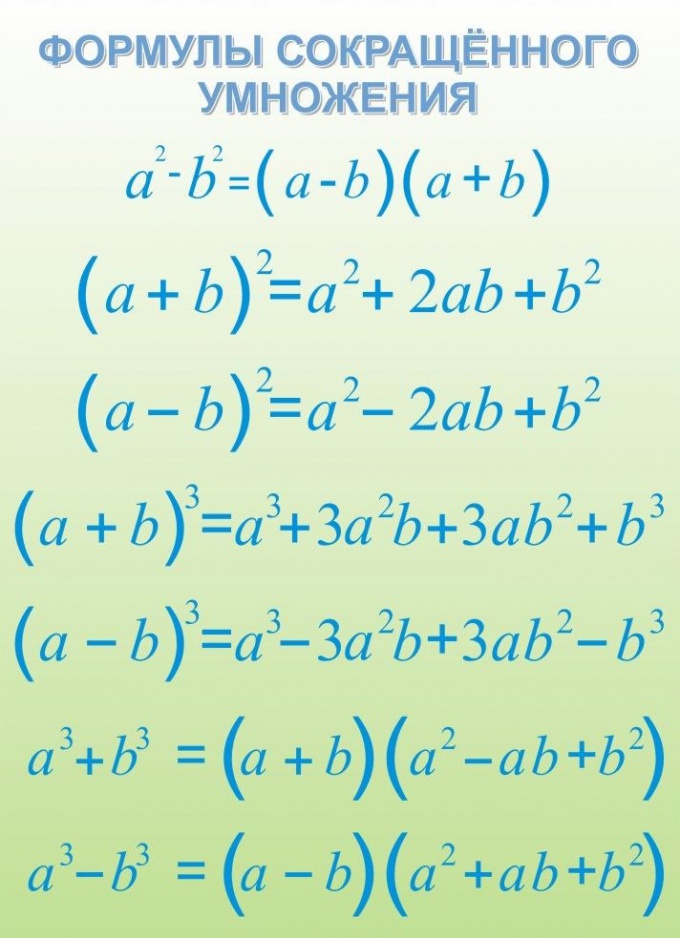Вам понадобится
- - понятие одночлена многочлена;
- - формулы сокращенного умножения;
- - действия с дробями;
- - основные тригонометрические тождества.
Инструкция
1
Если в выражении имеются одночлены с одинаковыми множителями, найдите сумму коэффициентов при них и умножьте на единый для них множитель. Например, если есть выражение 2•а-4•а+5•а+а=(2-4+5+1)∙а=4∙а.
2
3
В том случае, если выражение представляет собой натуральную дробь, выделите из числителя и знаменателя общий множитель и сократите дробь на него. Например, если нужно сократить дробь (3•a²-6•a•b+3•b²)/(6∙a²-6∙b²), вынесите из числителя и знаменателя общие множители в числителе это будет 3, в знаменателе 6. Получите выражение (3•(a²-2•a•b+b²))/(6∙(a²-b²)). Сократите числитель и знаменатель на 3 и примените к оставшимся выражениям формулы сокращенного умножения. Для числителя это квадрат разности, а для знаменателя разность квадратов. Получите выражение (a-b)²/(2∙ (a+b)∙(a-b)) сократив его на общий множитель a-b, получите выражение (a-b)/(2∙ (a+b)), которое при конкретных значениях переменных гораздо легче посчитать.
4
Если одночлены имеют одинаковые множители, возведенные в степень, то при их суммировании следите, чтобы степени были равны, иначе сводить подобные нельзя. Например, если есть выражение 2∙m²+6•m³-m²-4•m³+7, то при сведении подобных получится m²+2•m³+7.
5
При упрощении тригонометрических тождеств используйте формулы для их преобразования. Основное тригонометрическое тождество sin²(x)+cos²(x)=1, sin(x)/cos(x)=tg(x), 1/ tg(x)= ctg(x), формулы суммы и разности аргументов, двойного, тройного аргумента и другие. Например, (sin(2∙x)- cos(x))/ ctg(x). Распишите формулу двойного аргумента и котангенса, как отношения косинуса на синус. Получите (2∙ sin(x)• cos(x)- cos(x))• sin(x)/cos(x). Вынесите общий множитель, cos(x) и сократите дробь cos(x)•(2∙ sin(x) - 1)• sin(x)/cos(x)= (2∙ sin(x) - 1) • sin(x).
Видео по теме
Источники:
- формула упрощения выражения