Как найти уравнение прямой

Часто известно, что y зависит от x линейно, и дан график этой зависимости. В этом случае возможно узнать уравнение прямой. Сначала нужно выбрать на прямой две точки.

Инструкция

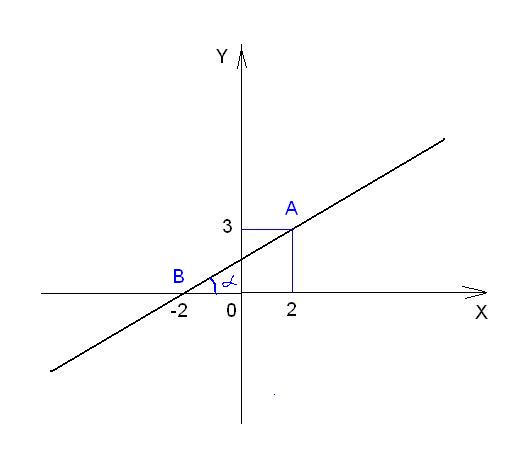
1. На рисунке мы выбрали точки А и B. Удобно выбирать точки пересечения с осями. Двух точек достаточно для того, чтобы точно определить прямую.
   
2. Найдите координаты выбранных точек. Для этого опустите перпендикуляры от точек на оси координат и запишите цифры со шкалы. Так для точки B из нашего примера координата x равна -2, а координата y - 0. Аналогичным образом для точки А координаты будут (2;3).
3. Известно, что уравнение прямой имеет вид y = kx + b. Подставляем в уравнение в общем виде координаты выбранных точек, тогда для точки A получим такое уравнение: 3 = 2k +b. Для точки B получим другое уравнение: 0 = -2k + b. Очевидно, что у нас система из двух уравнений с двумя неизвестными: k и b.
   
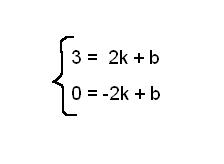
4. Дальше решаем систему любым удобным способом. В нашем случае можно сложить уравнения системы, так как неизвестная k входит в оба уравнения с коэффициентами, которые одинаковы по модулю, но противоположны по знаку. Тогда получим 3 + 0 = 2k - 2k + b + b, или, что то же: 3 = 2b. Таким образом b = 3/2. Подставим найденное значение b в любое из уравнений, чтобы найти k. Тогда 0 = -2k + 3/2, k = 3/4.
5. Подставим найденные k и b в уравнение общего вида и получим искомое уравнение прямой: y = 3x/4 + 3/2.