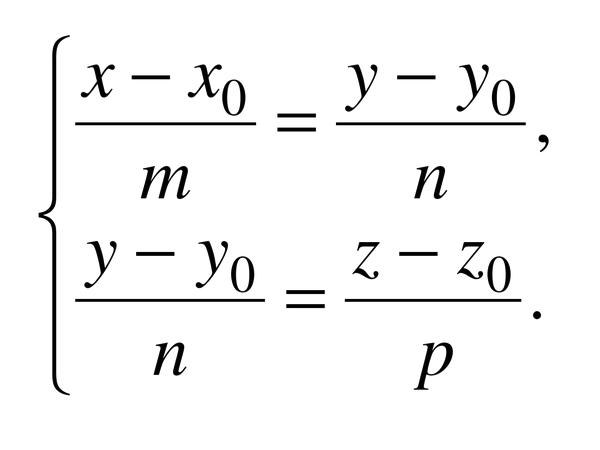Инструкция
1
Основа любых построений в геометрии – понятие расстояния между двумя точками в пространстве. Прямая – это линия, параллельная этому расстоянию, и эта линия бесконечна. Через две точки можно провести только одну прямую.
2
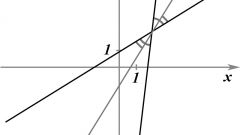
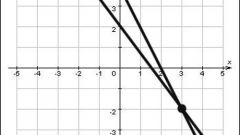
Графически прямая изображается в виде линии с неограниченными концами. Прямую нельзя изобразить целиком. Тем не менее, это принятое схематичное изображение подразумевает уход прямой в бесконечность в обе стороны. Прямую обозначают на графике строчными латинскими буквами, например, a или c.
3
Аналитически прямая в плоскости задается уравнением первой степени, в пространстве – системой уравнений. Различают общее, нормальное, параметрическое, векторно-параметрическое, тангенциальное, каноническое уравнения прямой через декартову систему координат.
4
Каноническое уравнение прямой вытекает из системы параметрических уравнений.Параметрические уравнения прямой записываются в следующем виде: X = x_0 + a*t; y = y_0 + b*t.
5
В этой системе приняты следующие обозначения: - x_0 и y_0 – координаты некоторой точки N_0, принадлежащей прямой;- a и b – координаты направляющего вектора прямой (принадлежащего или параллельного ей); - x и y – координаты произвольной точки N на прямой, причем вектор N_0N коллинеарен направляющему вектору прямой;- t – параметр, величина которого пропорциональна расстоянию от начальной точки N_0 до точки N (физический смысл этого параметра – время прямолинейного движения точки N вдоль направляющего вектора, т.е. при t=0 точка N совпадает с точкой N_0).
6
Итак, каноническое уравнение прямой получается из параметрического путем деления одного уравнения на другое методом исключения параметра t:(x – x_0)/(y – y_0) = a/b.Откуда:(x – x_0)/a = (y – y_0)/b.
7
Каноническое уравнение прямой в пространстве задается тремя координатами, следовательно:(x – x_0)/a = (y – y_0)/b = (z – z_0)/c, где c – аппликата направляющего вектора. При этом a^2 + b^2 + c^2 ? 0.