Инструкция
1
Прямая и плоскость – два взаимосвязанных геометрических понятия. Через любые две точки плоскости можно провести прямую линию, состоящую из ее же точек. А любая прямая принадлежит какой-либо плоскости. Любая фигура в геометрии – совокупность пересекающихся линий и ограниченных ими участков поверхности, от простейших треугольника и окружности до нестандартных выпуклых многоугольников и призм.
2
Для каждой прямой в пространстве можно найти проекцию на некоторую плоскость. Таким образом, можно вычислить угол между ними, как смежный к углу, образованному векторами направления и нормали. Например, пусть задано каноническое уравнение прямой L и общее уравнение плоскости P:
L: (х – х0)/p = (у – у0)/r = (z – z0)/s;
P: А•х + B•у + С•z + D = 0.
L: (х – х0)/p = (у – у0)/r = (z – z0)/s;
P: А•х + B•у + С•z + D = 0.
3
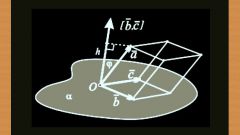
Коэффициенты этих уравнений – координаты вектора направления прямой и вектора нормали для плоскости. Тогда задача определения угла между прямой линией и ее проекцией сводится к поиску смежного угла между этими векторами. Смежный угол в данной ситуации составляет в сумме с искомым 90° или π/2. Найдите косинус угла (π/2 – α) по известной формуле:
cos (π/2 – α) = sin α = |p•А + r•B + s•C|/(√(p² + r² + s²)•√(А² + B² + C²)).
cos (π/2 – α) = sin α = |p•А + r•B + s•C|/(√(p² + r² + s²)•√(А² + B² + C²)).
4
Частные случаи, когда этот угол равен 90° или 180°, являются доказательством их перпендикулярности или параллельности. Тогда:
• если А/p = B/r = С/s – прямая перпендикулярна плоскости;
• если А•р + B•r + С•s = 0 – прямая параллельна плоскости.
• если А/p = B/r = С/s – прямая перпендикулярна плоскости;
• если А•р + B•r + С•s = 0 – прямая параллельна плоскости.
5
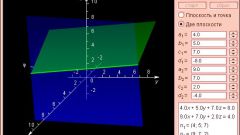
Пример: найти угол между прямой (х - 1)/4 = (у + 3)/-2 = (z - 8)/1 и плоскостью 5•х + 3•у – 4•z = 0.
Решение
Выпишите координаты вектора направления прямой – (4, -2, 1) и нормального вектора плоскости – (5, 3, -4). Подставьте все значения в формулу синуса угла:
sin α = |20 – 6 - 4|/(√(16 + 4 + 1)•√(25 + 9 + 16)) ≈ 0,3.
Решение
Выпишите координаты вектора направления прямой – (4, -2, 1) и нормального вектора плоскости – (5, 3, -4). Подставьте все значения в формулу синуса угла:
sin α = |20 – 6 - 4|/(√(16 + 4 + 1)•√(25 + 9 + 16)) ≈ 0,3.
6
Вычислите арксинус получившейся величины, чтобы определить искомый угол α:
α = аrсsin 0,3 ≈ 17,46°.
α = аrсsin 0,3 ≈ 17,46°.
Видео по теме