Инструкция
1
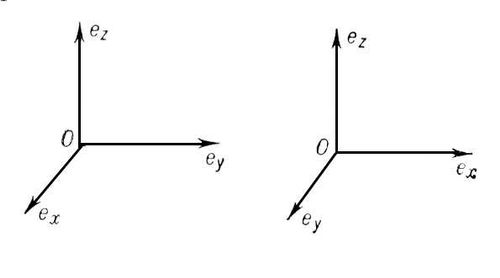
Система координат называется прямоугольной (ортогональной), если ее оси координат взаимно перпендикулярны. Если при этом они еще и поделены на равные по длине отрезки (единицы измерения), то такая система координат называется декартовой (ортонормированной).В курс средней школы входит рассмотрение двухмерной и трехмерной декартовой системы координат. Если т. О – начало отсчета, то ось OX – абсцисса, OY – ордината, OZ – аппликата.
2
Рассмотрим простой пример вычисления координат для точек пересечения двух заданных окружностей.
Пусть O1, O2 – центры окружностей с заданными координатами (x1;y1), (x2;y2) и известными радиусами R1, R2 соответственно.
3
Нужно найти координаты точек пересечения данных окружностей A(x3;y3), B(x4;y4), причем т.D – точка пересечения отрезков O1O2 и AB.
4
Решение: для удобства примем, что центр первой окружности O1 совпадает с началом координат. Далее будем рассматривать простое пересечение окружности и прямой, проходящей через отрезок AB.
5
Согласно уравнению окружности R2 = (x1-x0)2 + (y1-y0)2,
где O(x0;y0) – центр окружности, A(x1; y1) – точка на окружности,
составим систему уравнений при x1, y1 равных нулю:
R12 = O1O2+OA2 = x3 + y32,
R22 = O1O2+OA2 = (x3 - x2)2 + (y 3 - y 2)2
6
Решив систему, найдем координаты точки A, аналогично находятся координаты точки B.