Как найти координаты вектора в базисе

Пара точек называется упорядоченной, если про них известно, какая из точек является первой, а какая – второй. Отрезок с упорядоченными концами называется направленным отрезком или вектором. Базисом в векторном пространстве называется такая упорядоченная линейно независимая система векторов, что любой вектор пространства раскладывается по ней. Коэффициенты при данном разложении являются координатами вектора в этом базисе.

Инструкция

1. Пусть имеется система векторов a1,a2,…,ak. Она линейно независима, когда нулевой вектор раскладывается по ней единственным образом. Другими словами, только тривиальная комбинация этих векторов даст своим результатом нулевой вектор. Тривиальное разложение предполагает равенство нулю всех коэффициентов.
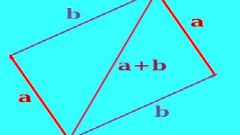
2. Система, состоящая из одного ненулевого вектора, всегда линейно независима. Система из двух векторов линейно независима, если они не коллинеарны. Чтобы система из трех векторов была линейно независимой, необходимо, чтобы они были некомпланарными. Из четырех и более векторов уже невозможно составить линейно независимую систему.
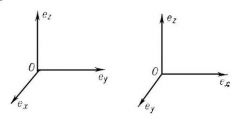
3. Таким образом, в нулевом пространстве базиса нет. В одномерном пространстве базисом может быть любой ненулевой вектор. В пространстве размерностью два базисом может стать любая упорядоченная пара неколлинеарных векторов. Наконец, упорядоченная тройка некомпланарных векторов сформирует базис для трехмерного пространства.
4. Вектор можно разложить по базису, например, p= λ1•a1+ λ2•a2+…+ λk•ak. Коэффициенты при разложении λ1,…, λk являются координатами вектора в этом базисе. Иногда они называются также компонентами вектора. Поскольку базис являет собой линейно независимую систему, коэффициенты разложения определены однозначно и единственным образом.
5. Пусть имеется базис, состоящий из одного вектора e. У любого вектора в этом базисе будет только одна координата: p=a•e. Если p сонаправлен базисному вектору, число a покажет соотношение длин векторов p и e. Если противоположно направлен, число a будет еще и отрицательным. В случае произвольного направления вектора p по отношению к вектору e в компоненту a будет входить косинус угла между ними.
6. В базисе более высоких порядков разложение будет представлять более сложное уравнение. Тем не менее, можно последовательно разложить заданный вектор по векторам базиса, аналогично одномерному.
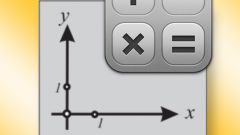
7. Чтобы найти координаты вектора в базисе, поместите на чертеже вектор рядом с базисом. Если необходимо, начертите проекции вектора на координатные оси. Сравните длину вектора с базисом, распишите углы между ним и базисными векторами. Используйте для этого тригонометрические функции: синус, косинус, тангенс. Разложите вектор по базису, а коэффициенты при разложении будут его координатами.