Вам понадобится
  • - система координат;
  • - линейка;
  • - транспортир.
Инструкция
1
Если вектор находится на плоскости, то его начало и конец имеют координаты (x1;y1), (x2;y2). Чтобы найти его длину произведите следующие математические операции:: 1. Найдите координаты вектора, для чего из координат конца вектора, отнимаем координаты начала x=x2-x1, y=y2-y1.2. Возведите каждую из координат в квадрат и найдите их сумму x²+y². 3. Из числа, полученного при выполнении п.2, извлеките корень квадратный. Это и будет длина вектора, расположенного на плоскости.
2
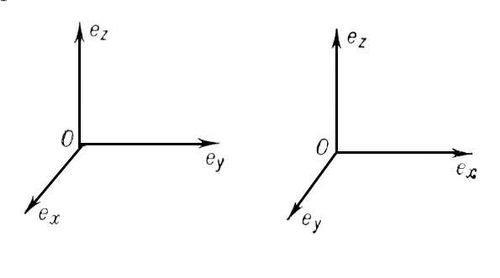
В том случае если вектор располагается в пространстве, он имеет три координаты x, y и z, которые вычисляются по тем же правилам, что и для вектора, расположенного на плоскости. Найдите его длину, сложив квадраты всех трех координат, и извлеките из результата сложения корень квадратный.
3
Если известна одна из координат вектора и угол между ним и осью ОХ (если известен угол между осью OY и вектором то, чтобы найти искомый угол, отнимите его от 90º), найдите длину из соотношений, которые характеризуют полярные координаты: 1. длина вектора равна отношению координаты x к косинусу данного угла; 2. длина вектора равна отношения координаты y к синусу данного угла.
4
Чтобы найти длину вектора, который представляет собой сумму двух векторов, найдите его координаты, сложив соответствующие координаты, а затем найдите длину вектора, координаты которого известны.
5
Если же координаты векторов неизвестны, а известны только длины, перенесите один из векторов так, чтобы он начинался в той точке, где заканчивается второй. Измерьте угол между ними. Затем от суммы квадратов длин векторов отнимите их удвоенное произведение, умноженное на косинус угла между ними. Из полученного числа извлеките корень квадратный. Это и будет длина вектора, который является суммой двух векторов. Постройте его, соединив начало второго вектора с концом первого.