Вам понадобится
  • - бумага;
  • - ручка.
Инструкция
1
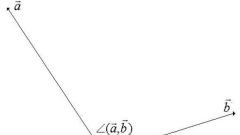
В полярной системе координат их изображают радиус-векторами точек его конца (начало находится в начале координат). Векторы принято обозначать следующим образом (см. рис.1). Длина вектора или его модуль обозначается |a|. В декартовых координатах вектор задается координатами его конца. Если а имеет некоторые координаты (x, y, z), то записи вида а (x, y, a)= а={x, y, z} необходимо считать равнозначными. При использовании векторов-ортов координатных осей i, j, k, координаты вектора а будут иметь следующий вид: а=xi + yj + zk.
Как вычислить скалярное произведение векторов
2
Скалярным произведением векторов a и b называется число (скаляр) равное произведению модулей этих векторов на косинус угла между ними (см. рис. 2): (a, b) = |a||b|cosα.
Скалярное произведение векторов обладает следующими свойствами:
1. (a, b)=(b,a);
2. (a+ b,c)=(a,c)+(b,c);
3. |a|2=(a,a) – скалярный квадрат.
Если два вектора расположены под углом 90 градусов по отношению друг к другу (ортогональны, перпендикулярны), то их скалярное произведение равно нулю, так как косинус прямого угла равен нулю.
3
Пример. Необходимо найти скалярное произведение двух векторов, заданных в декартовых координатах.
Пусть а={x1, y1, z1}, b={x2, y2, z2}. Или а=x1i + y1j + z1k, b=x2 i + y2 j + z2k.
Тогда (a, b)=(x1i + y1j + z1k, x2 i + y2 j + z2k)=(x1x2) (i, i)+ (x1y2) (i, j)+ (x1z2) (i, k) + (y1x2) (j, i)+ (y1y2) (j, j)+
+(y1z2) (j, k) + (z1x2) (i, i)+ (z1y2) (i, j)+ (z1z2) (i, k).
4
В этом выражении от нуля отличны только скалярные квадраты, так как разноименные координатные орты ортогональны. С учетом того, что модуль любого вектора-орта (то же и для i, j, k) – единица, имеем (i,i)=(j,j)= (k,k)=1. Таким образом, от исходного выражения осталось (a, b)=x1x2 + y1y2 + z1z2.
Если задать координаты векторов некоторыми числами, то получим следующее:
а={10, -3, 1}, b={-2, 5, -4}, тогда (a, b)=x1x2 + y1y2 + z1z2=-20-15-4=-39.