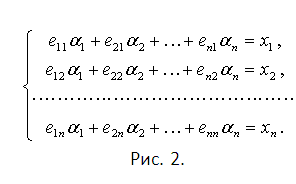Инструкция
1
Обосновать линейную независимость системы векторов очень просто. Составьте определитель, строки которого состоят из их «координат», и вычислите его. Если этот определитель отличен от нуля, то и векторы линейно независимы. Не забывайте, что размерность определителя может быть достаточно большой, и находить его придется разложением по строке (столбцу). Поэтому применяйте предварительные линейные преобразования (лучше только строк). Оптимальный случай – это доведение определителя до треугольного вида.
2
Например, для системы векторов е1=(1, 2, 3), e2=(2, 3, 2), e3(4, 8, 6) соответствующий определитель и его преобразования представлены на рисунке 1. Здесь на первом шаге первая строка умножалась на два и вычиталась из второй. Затем она умножалась она на четыре и вычиталась из третьей. На втором шаге вторая строка складывалась с третьей. Так как ответ отличен от нуля, то заданная система векторов линейно независима.
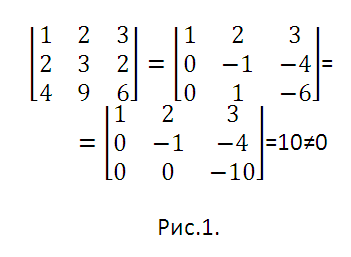
3
Теперь следует перейти к задаче разложения вектора по базису в R^n. Пусть базисные векторыe1=(e1, e21, … ,en1), e2=(e21, e22, … ,en2), … , en=(en1, en2, … , enn), а вектор x задан координатами в каком-либо другом базисе того же пространства R^n x=(x1, x2, … ,xn). При этом его можно представить в виде х=a1e1+a2e2+…+anen, где (a1, a2, … ,an) коэффициенты искомого разложения х по базису (e1, e2, … , en).
4
Последнюю линейную комбинацию перепишите подробнее, подставляя вместо векторов соответствующие наборы чисел: (x1, x2,…, xn)=a1(e11, e12,..,e1n)+ a2(e21, e22,..,e2n)+…+ an(en1, en2,..,enn). Полученное перепишите в виде системы n линейных алгебраических уравнений с n неизвестными (a1, a2, … ,an) (см. рис. 2). Так как векторы базиса линейно независимы, то система имеет единственное решение (a1, a2, … ,an). Разложение вектора по заданному базису найдено.