Как доказать, что вектора образуют базис

Базисом в n-мерном пространстве называется такая система из n векторов, когда все остальные векторы пространства можно представить в виде комбинации векторов, входящих в базис. В трехмерном пространстве в любой базис входят три вектора. Но не любые три образуют базис, поэтому и существует задача проверки системы векторов на возможность построения из них базиса.

Вам понадобится

• - умение вычислять определитель матрицы

Инструкция

1. Пусть в линейном n-мерном пространстве существует система векторов e1, е2, е3, ... , еn. Их координаты: e1 = (e11; e21; e31; ... ; en1), е2 = (е12; е22; е32; ... ; еn2), ... , еn = (e1n; e2n; e3n; ... ; enn). Чтобы узнать, образуют ли они базис в этом пространстве, составьте матрицу со столбцами e1, е2, е3, ... , еn. Найдите ее определитель и сравните его с нулем. Если определитель матрицы из этих векторов не равен нулю, то такие векторы образуют базис в данном n-мерном линейном пространстве.
2. Например, пусть даны три вектора в трехмерном пространстве a1, a2 и a3. Их координаты: а1 = (3; 1; 4), а2 = (-4; 2; 3) и а3 = (2; -1; -2). Надо выяснить, образуют ли эти вектора базис в трехмерном пространстве. Составьте матрицу из векторов, как показано на рисунке.
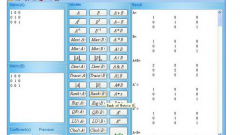
3. Вычислите определитель получившейся матрицы. На рисунке показан простой способ вычисления определителя матрицы 3 на 3. Элементы, соединенные линией, следует перемножить. При этом произведения, обозначенные красной линией входят в общую сумму со знаком "+", а соединенные синей линией - со знаком "-". det A = 3*2*(-2) + 1*2*3 + 4*(-4)*(-1) - 2*2*4 - 1*(-4)*(-2) - 3*3*(-1) = -12 + 6 + 16 - 16 - 8 + 9 = -5 -5≠0, следовательно, а1, а2 и а3 образуют базис.