Вам понадобится
- - ручка;
- - бумага.
Инструкция
1
Такое перемножение называют «строка на столбец».
Умножение матрицы А на В определено в случае равенства числа столбцов А числу строк В. Операция умножения обозначается как и обычное арифметическое действие – знаком «×» или просто АВ. Если С=АВ, то ее элементы будут перемножаться по следующему правилу (см. рис.1.):
Умножение матрицы А на В определено в случае равенства числа столбцов А числу строк В. Операция умножения обозначается как и обычное арифметическое действие – знаком «×» или просто АВ. Если С=АВ, то ее элементы будут перемножаться по следующему правилу (см. рис.1.):
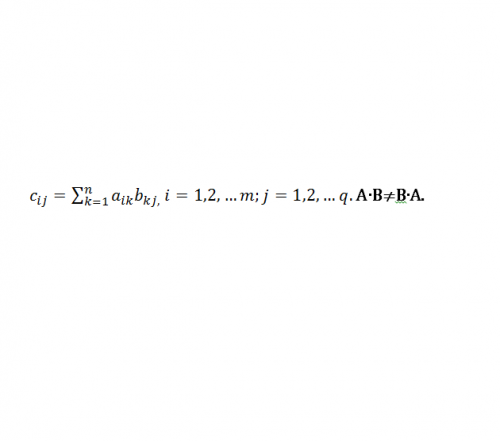
2
Для каждой невырожденной квадратной матрицы А (определитель |A| не равен нулю) существует единственная обратная матрица, обозначаемая А^-1,
такая, что А^-1×А=А А^(-1)=Е.
Матрица Е называется единичной, она состоит из единиц на главной диагонали, остальное элементы – нули. А^(-1) вычисляется по следующему правилу (см. рис.2.):
такая, что А^-1×А=А А^(-1)=Е.
Матрица Е называется единичной, она состоит из единиц на главной диагонали, остальное элементы – нули. А^(-1) вычисляется по следующему правилу (см. рис.2.):
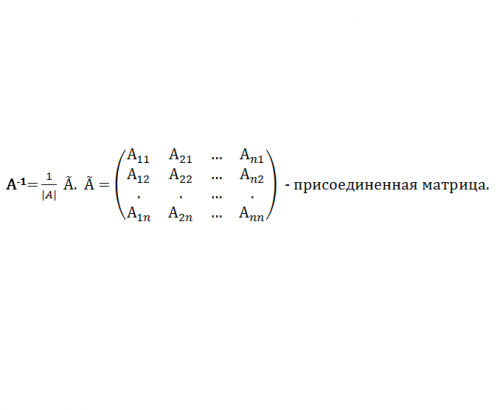
3
Здесь Аij – алгебраическое дополнение соответствующего элемента определителя матрицы А. Аij получают удалением из определителя |A| i-строки и j-столбца, на пересечении которых лежит а(ij), и умножением вновь полученного определителя на (-1)^(i+j).
Фактически присоединенная матрица – это транспонированная матрица из алгебраических дополнений элементов матрицы А. Транспонирование – это замена столбцов матрицы на строки (и наоборот). А транспонированная обозначается А^Т.
Фактически присоединенная матрица – это транспонированная матрица из алгебраических дополнений элементов матрицы А. Транспонирование – это замена столбцов матрицы на строки (и наоборот). А транспонированная обозначается А^Т.

4
Пример 1. Найти обратную матрицу для A^(-1) (см. рис.3).

5
Матричные уравнения исторически появились в связи с необходимостью получения компактных алгоритмов решения систем линейных уравнений. Вид такой системы (см. рис.4.)
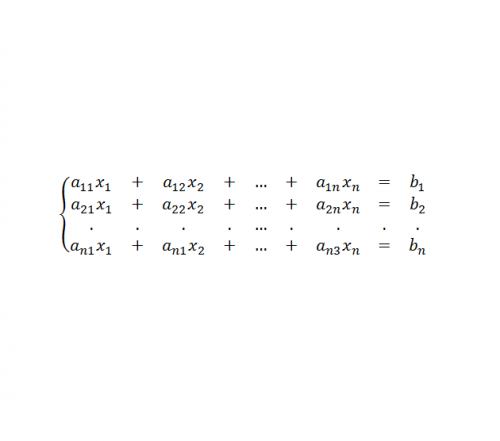
6
Если ввести понятие матрицы коэффициентов этой системы A=(a(ij)), i=1,2,…,n; j=1,2,…,n матрицы-столбца переменных Х=(x1, x2,…,xn)^T и матрицы столбца правых частей B=(b1, b2,…,bn)^Т, то компактно в матричной форме система уравнений запишется в виде АХ=В. Дальнейшее решение состоит в умножении этого уравнения на обратную матрицу А^(-1) слева. Получаем (АА^(-1))Х=А^(-1)В, ЕХ=А^(-1)В, Х=А^(-1)В.
Пример 2. Используя матрицу коэффициентов А предыдущего примера №1, найти решение матричного уравнения, в котором В= (6, 12, 0)^T. Тогда Х=А^(-1)В. А^(-1) уже найдено в предыдущем примере (см. рис.5).
Пример 2. Используя матрицу коэффициентов А предыдущего примера №1, найти решение матричного уравнения, в котором В= (6, 12, 0)^T. Тогда Х=А^(-1)В. А^(-1) уже найдено в предыдущем примере (см. рис.5).
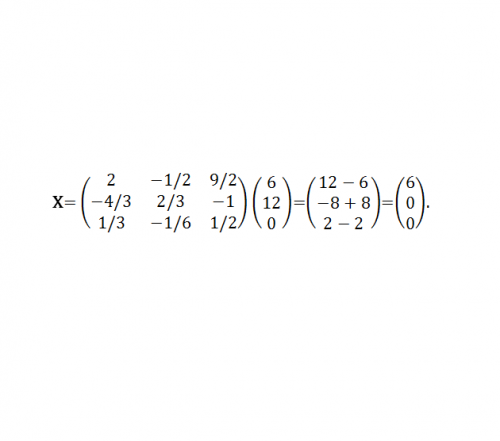
7
Или х1=6, х2=0 , х3=0.
В предложенной выше системе АХ=В матрицы Х и В могут быть не только матрицами-столбцами, но и имеющими большую размерность. Например, (см. рис.6)
В предложенной выше системе АХ=В матрицы Х и В могут быть не только матрицами-столбцами, но и имеющими большую размерность. Например, (см. рис.6)
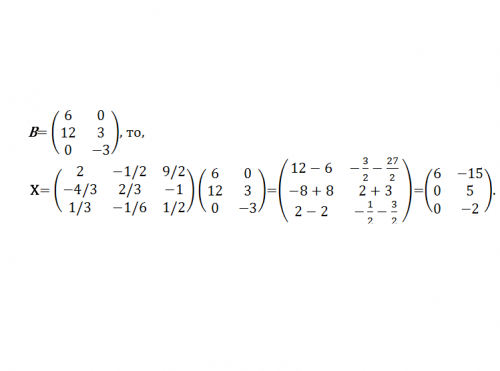
Видео по теме