Инструкция
1
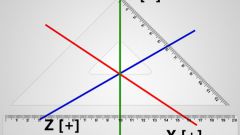
Обратите внимание на то, что вычисление угла между двумя любыми векторами сводится к нахождению такого между векторами, имеющими общую точку. Это часто вызывает непонимание, однако объясняется достаточно просто. Чтобы два лежащих в одной плоскости вектора начинались в одной точке, вам необходимо совершить операцию параллельного переноса. Но эта процедура никак не влияет на искомую величину.
2
Запомните общее определение угла между двумя векторами: это поможет вам сложить представление о том, что требуется в задаче. Ведь угол – это не цифры, а определенная реальность, обозначающая ту кратчайшую величину, на которую необходимо повернуть один вектор (относительно своей начальной точки) до сонаправленности со вторым. Важно учитывать, что искомая величина угла должна быть в пределах от нуля до 3,14 радиан.
3
Не забывайте, что если вы имеете дело с коллинеарными или параллельными векторами, величина угла составляет ноль градусов в случае их сонаправленности и 180 – для разнонаправленных векторов. Это следует из определения, так как вам необходимо повернуть второй вектор, чтобы поменять его направление.
4
Воспользуйтесь простой формулой, позволяющей быстро вычислить величину косинуса угла между векторами. Для этого вам необходимо знать соответствующие координаты. Косинус угла представляет собой дробь, в числителе которой стоит скалярное произведение векторов, а в знаменателе – произведение их модулей. Для нахождения первой величины для векторов с координатами а1, а2, а3 и с1, с2, с3, найдите сумму произведений а1с1, а2с2, а3с3. Модуль каждого вектора есть корень второй степени из суммы квадратов его координат.
5
Обратитесь к помощи электронных калькуляторов, которые по заданным параметрам векторов вычислят требуемый угол.
Видео по теме