Вам понадобится
- Знания по геометрии.
Инструкция
1
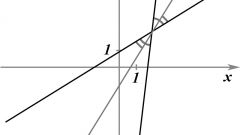
Пусть даны две прямые с уравнениями Ax + By = C и Dx + Ey = F. Выразим из этих уравнений прямых коэффициент угла наклона. Для первой прямой этот коэффициент равен A/B, а для второй D/E соответственно. Для наглядности рассмотрим пример. Уравнение первой прямой 4x+6y=20, уравнение второй прямой -3x+5y=3. Коэффициенты угла наклона будут соответственно равны: 0.67 и -0.6.
2
Теперь необходимо найти угол наклона каждой прямой. Для этого посчитаем арктангенс от углового коэффициента. В рассматриваемом примере углы наклона прямых будут равны arctg(0.67) = 34 градуса и arctg(-0.6) = -31 градус соотвественно.
3
Так одна прямая умеет отрицательный угловой коэффициент, а вторая положительный, то угол между этими прямыми будет равен сумме абсолютных величин этих углов. В случае же, когда угловые коэффициенты оба отрицательны или оба положительны, то угол находится путем вычитания из большего угла меньшего. В рассматриваемом примере получим, что угол между прямыми равен |34| + |-31| = 34 + 31 = 65 градусов.
Обратите внимание
Период тригонометрической функции тангенс равен 180 градусам, а значит углы наклоны прямых не могут, по модулю, превышать этого значения.
Полезный совет
Если угловые коэффициенты равны между собой, то угол между такими прямыми равен 0, так как такие прямые или совпадают или параллельны.