Как вычесть вектор

Операция вычитания векторов, как и вычитание обычных чисел, обозначает действие, обратное операции сложения. Для обычных чисел это означает, что одно из слагаемых превращается в свою противоположность (его знак меняется на противоположный), а остальные действия осуществляются по тем же правилам, что и при обычном сложении. Для операции вычитания векторов нужно действовать также - сделать один из них (вычитаемый) своей противоположностью (поменять направление), а затем применить обычные правила сложения векторов.

Инструкция

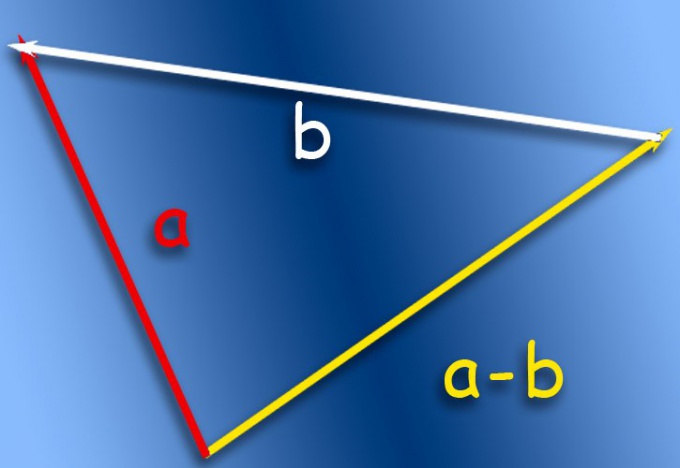
1. Если вычитание надо отобразить на бумаге, то воспользуйтесь, например, правилом треугольника. Оно описывает операцию сложения векторов, а для того, чтобы применить ее к операции вычитания надо внести соответствующие поправки, касающиеся вычитаемого вектора. Его начало и конец надо поменять местами, то есть инвертировать вектор, и этим поменять его знак, чтобы операция сложения стала операцией вычитания.
2. Перенесите вычитаемый вектор параллельно самому себе таким образом, чтобы его окончание совпало с окончанием уменьшаемого вектора. Затем соедините начало перенесенного вектора с началом уменьшаемого и поставьте стрелку в том конце отрезка, который совпадает с началом перенесенного вектора. Этот вектор с началом, совпадающим с началом уменьшаемого вектора, и окончанием в начале перенесенного вектора и будет результатом операции вычитания.
3. Используйте правило параллелограмма (с поправкой на инвертирование вычитаемого вектора) в качестве альтернативы правилу треугольника. Для этого перенесите вычитаемый вектор параллельно самому себе таким образом, чтобы его окончание совпадало с началом уменьшаемого вектора. Таким способом вы получите две стороны геометрической фигуры - параллелограмма. Достройте его недостающие стороны и проведите диагональ из точки, которая является концом вычитаемого и началом уменьшаемого векторов. Эта диагональ и будет вектором, полученным в результате вычитания.
4. Если уменьшаемый и вычитаемый векторы заданы не графически, а координатами своих конечных точек в двухмерной или трехмерной системе координат, то и результат вычитания можно представить в таком же виде. Для этого просто отнимите значения координат вычитаемого вектора от соответствующих значений координат уменьшаемого вектора. Например, если вектор A (уменьшаемый) задан координатами (Xa;Ya;Za), а вектор B (вычитаемый) - координатами (Xb;Yb;Zb), то результатом операции вычитания A-B будет вектор C с координатами (Xa-Xb; Ya-Yb; Za-Zb).