Как найти произведение векторов

Для векторов есть два понятия произведения. Одно из них скалярное произведение, другое - векторное. Каждое из этих понятий имеет свой математический и физический смысл и вычисляется совершенно по-разному.

Инструкция

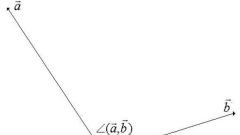
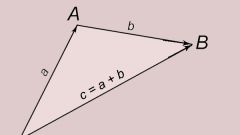
1. Рассмотрим два вектора в трехмерном пространстве. Вектор a с координатами (xa; ya; za) и вектор b с координатами (xb; yb; zb). Скалярное произведение векторов а и b обозначается (a,b). Оно вычисляется по формуле: (a,b) = |a|*|b|*cosα, где α - угол между двумя векторами.Можно вычислить скалярное произведение в координатах: (a,b) = xa*xb + ya*yb + za*zb. Также существует понятие скалярного квадрата вектора, это скалярное произведение вектора на самого себя: (a,a) = |a|² или в координатах (a,a) = xa² + ya² + za².Скалярное произведение векторов - это число, характеризующее местоположение векторов относительно друг друга. Часто его используют для вычисления угла между векторами.
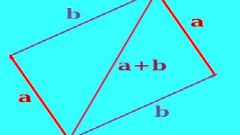
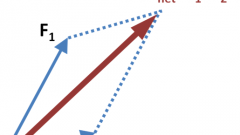
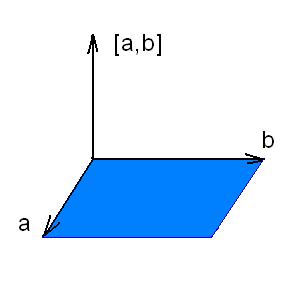
2. Векторное произведение векторов обозначается [a,b]. В результате векторного произведения получается вектор, который перпендикулярен обоим векторам-сомножителям, а длина этого вектора равна площади параллелограмма, построенного на векторах-сомножителях. Причем три вектора a, b и [a,b] образуют так называемую правую тройку векторов.Длина вектора [a,b] = |a|*|b|*sinα, где α - угол между векторами a и b.