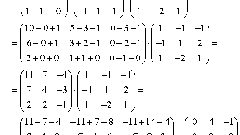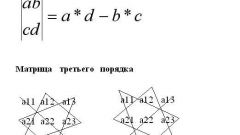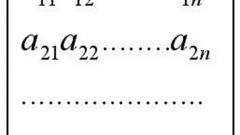Инструкция
1
По определению матрица C, произведение матриц A и B, состоит из элементов с[i,j], каждый из которых равен сумме произведений элементов строки i матрицы A на соответствующие элементы столбца j матрицы B. Это можно записать формулой. В формуле учитывается, что матрица A имеет размерность m x p, а матрица B - p x n. Тогда матрица C будет иметь размерность m x n.
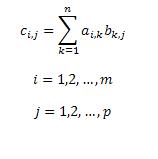
2
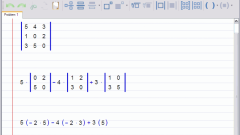
Рассмотрим пример. Перемножим матрицы A и B, указанные на рисунке. Последовательно найдем все элементы матрицы C = AB.
с[1,1] = a[1,1]*b[1,1] + a[1,2]*b[2,1] + a[1,3]*b[3,1] = 3*2 + 2*5 + 0*3 = 16
c[1,2] = a[1,1]*b[1,2] + a[1,2]*b[2,2] + a[1,3]*b[3,2] = 3*1 + 2*4 + 0*2 = 11
c[2,1] = a[2,1]*b[1,1] + a[2,2]*b[2,1] + a[2,3]*b[3,1] = 1*2 + 3*5 + 1*3 = 20
c[2,2] = a[2,1]*b[1,2] + a[2,2]*b[2,2] + a[2,3]*b[3,2] = 1*1 + 3*4 + 1*2 = 15
с[1,1] = a[1,1]*b[1,1] + a[1,2]*b[2,1] + a[1,3]*b[3,1] = 3*2 + 2*5 + 0*3 = 16
c[1,2] = a[1,1]*b[1,2] + a[1,2]*b[2,2] + a[1,3]*b[3,2] = 3*1 + 2*4 + 0*2 = 11
c[2,1] = a[2,1]*b[1,1] + a[2,2]*b[2,1] + a[2,3]*b[3,1] = 1*2 + 3*5 + 1*3 = 20
c[2,2] = a[2,1]*b[1,2] + a[2,2]*b[2,2] + a[2,3]*b[3,2] = 1*1 + 3*4 + 1*2 = 15
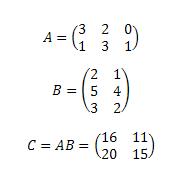
Обратите внимание
Квадратные матрицы можно перемножать в любом порядке, но результат AB будет отличаться от BA.
Если одна из матриц является диагональной и элементы, стоящие на ее диагонали равны, то в этом случае умножение ее на любую квадратную соответствующей размерности коммутативно: AD = DA.
Если одна из матриц является диагональной и элементы, стоящие на ее диагонали равны, то в этом случае умножение ее на любую квадратную соответствующей размерности коммутативно: AD = DA.