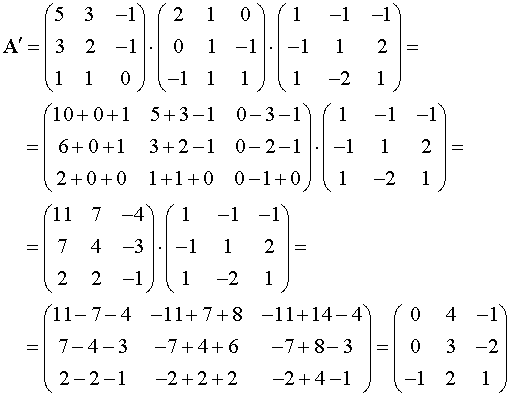Инструкция
1
Самая простая и краткая формулировка этой операции такова: матрицы перемножаются по алгоритму "строка на столбец".
Теперь подробнее об этом правиле, а также о возможных ограничениях и особенностях.
Умножение на единичную матриц переводит исходную матрицы саму в себя (эквивалентно умножению чисел, где один из элементов 1). Аналогично, умножение на нулевую матрицу даёт нулевую матрицу.
Главное условие, накладываемое на участвующие в операции матрицы вытекает из способа выполнения умножения: строк в первой матрице должно быть столько же, сколько столбцов во второй. Нетрудно догадаться, что в противном случае умножать будет просто не на что.
Также стоит отметить ещё один важный момент: у умножения матриц нет свойства коммутативности (или "перестановочности"), иначе говоря, А умножить на B не равняется B умножить на А. Запомните это и не путайте с правилом для умножения чисел.
Теперь подробнее об этом правиле, а также о возможных ограничениях и особенностях.
Умножение на единичную матриц переводит исходную матрицы саму в себя (эквивалентно умножению чисел, где один из элементов 1). Аналогично, умножение на нулевую матрицу даёт нулевую матрицу.
Главное условие, накладываемое на участвующие в операции матрицы вытекает из способа выполнения умножения: строк в первой матрице должно быть столько же, сколько столбцов во второй. Нетрудно догадаться, что в противном случае умножать будет просто не на что.
Также стоит отметить ещё один важный момент: у умножения матриц нет свойства коммутативности (или "перестановочности"), иначе говоря, А умножить на B не равняется B умножить на А. Запомните это и не путайте с правилом для умножения чисел.
2
Теперь, собственно сам процесс умножения.
Пусть мы умножаем матрицу А на матрицу B справа.
Берём первую строчку матрицы А и ее i-ый элемент умножаем на i-ый элемент первого столцба матрицы B. Все полученные произведения складываем и записываем на место а11 в итоговую матрицу.
Далее первую строку матрицы А аналогичным образом умножаем на второй столбец матрицы В, а получившийся результат записываем справа от первого полученного числа в итоговую матрицу, то есть на позицию а12.
Затем также поступаем с первой строкой матрицы А и 3-им, 4-ым и т.д. столбцами матрицы Б, заполнив, таким образом, первую строчку итоговой матрицы.
Пусть мы умножаем матрицу А на матрицу B справа.
Берём первую строчку матрицы А и ее i-ый элемент умножаем на i-ый элемент первого столцба матрицы B. Все полученные произведения складываем и записываем на место а11 в итоговую матрицу.
Далее первую строку матрицы А аналогичным образом умножаем на второй столбец матрицы В, а получившийся результат записываем справа от первого полученного числа в итоговую матрицу, то есть на позицию а12.
Затем также поступаем с первой строкой матрицы А и 3-им, 4-ым и т.д. столбцами матрицы Б, заполнив, таким образом, первую строчку итоговой матрицы.
3
Теперь переходим ко второй строке и снова перемножаем её последовательно на все столбцы, начиная с первого. Записываем результат во вторую строку итоговой матрицы.
Затем к 3-ей, 4-ой и т.д.
Повторяем действия, пока не перемножим все строки в матрице А со всеми столбцами матрицы В.
Затем к 3-ей, 4-ой и т.д.
Повторяем действия, пока не перемножим все строки в матрице А со всеми столбцами матрицы В.