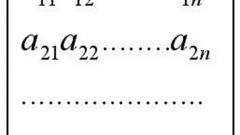Инструкция
1
В общем виде систему линейных алгебраических уравнений можно решить методом подстановки, но для СЛАУ большой размерности такое вычисление весьма трудоемко. И чаще в этом случае используют связанные матрицы, в том числе и расширенную.
2
Запишите заданную систему линейных уравнений. Проведите ее преобразование, упорядочив множители в уравнениях таким образом, чтобы одинаковые неизвестные переменные располагались в системе строго друг под другом. Свободные коэффициенты без неизвестных перенесите в другую часть уравнений. При перестановке слагаемых и переносе учитывайте их знак.
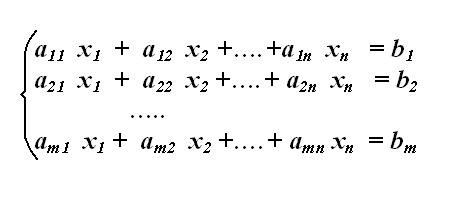
3
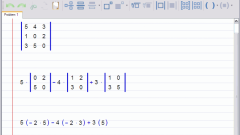
Определите матрицу системы. Для этого отдельно выпишите коэффициенты, стоящие при искомых переменных СЛАУ. Выписывать нужно в том порядке, как они расположены в системе, т.е. из первого уравнения первый коэффициент поставьте на пересечении первой строки и первого столбца матрицы. Порядок строк новой матрицы соответствует порядку уравнений системы. Если одна из неизвестных системы в данном уравнении отсутствует, значит, ее коэффициент здесь равен нулю – внесите ноль в матрицу на соответствующую позицию строки. Получаемая матрица системы должна быть квадратной (m=n).
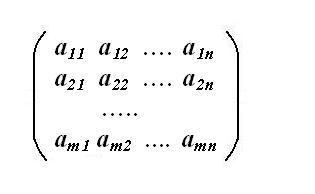
4
Найдите расширенную матрицу системы. Свободные коэффициенты в уравнениях системы за знаком равенства выпишите в отдельный столбец, сохраняя тот же порядок строк. В квадратной матрице системы справа от всех коэффициентов поставьте вертикальную черту. За чертой допишите полученный столбец свободных членов. Это и будет расширенная матрица исходной СЛАУ размерностью (m, n+1), где m – число строк, n – число столбцов.
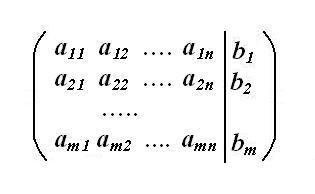
Обратите внимание
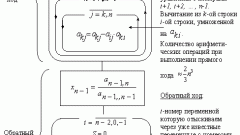
Именно по расширенной матрице согласно методу Гаусса вычисляются корни системы линейных алгебраических уравнений. Метод Гаусса является одним из наиболее активно используемых способов решения СЛАУ большого порядка.
Источники:
- расширенная матрица системы