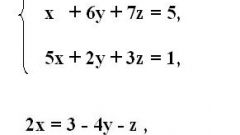Инструкция
1
Запишите основную матрицу системы. Для этого приведите уравнения в стандартный вид (то есть выставьте все коэффициенты в одном и том же порядке, если какого либо из них нет – запишите, просто с числовым коэффициентом «0»). Выпишите все коэффициенты в виде таблицы, заключите ее в скобки (свободные члены, перенесенные в правую часть, не учитывайте).
2
Точно также запишите расширенную матрицу системы, только в этом случае поставьте справа вертикальную черту и запишите столбик свободных членов.
3
Посчитайте ранг основной матрицы, это наибольший ненулевой минор. Минор первого порядка – это любая цифра матрицы, очевидно, что она не равна нулю. Чтобы посчитать минор второго порядка, возьмите любые две строки и любые два столбца (у вас получится таблица из четырех цифр). Посчитайте определитель, умножьте верхнее левое число на нижнее правое, вычтите из полученного числа произведение нижнего левого и верхнего правого. У вас получился минор второго порядка.
4
Сложнее посчитать минор третьего порядка. Для этого возьмите любые три строки и три столбца, у вас получится таблица из девяти чисел. Посчитайте определитель по формуле: ∆=а11а22а33+а12а23а31+а21а32а13-а31а22а13-а12а21а33-а11а23а32 (первая цифра коэффициента – номер строки, вторая цифра – номер столбца). Вы получили минор третьего порядка.
5
Если в вашей системе четыре или более уравнений, посчитайте также миноры четвертого (пятого и т.д.) порядков. Выберите самый большой, не равный нулю минор – это и будет ранг основной матрицы.
6
Точно так же найдите ранг расширенной матрицы. Обратите внимание, если количество уравнений в вашей системе совпадает с рангом (например, три уравнения, и ранг равен 3), рассчитывать ранг расширенной матрицы нет смысла – очевидно, что он также будет равен этому числу. В таком случае можно смело делать вывод о том, что система линейных уравнений совместна.
Видео по теме