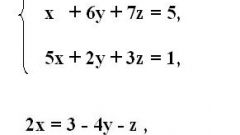Инструкция
1
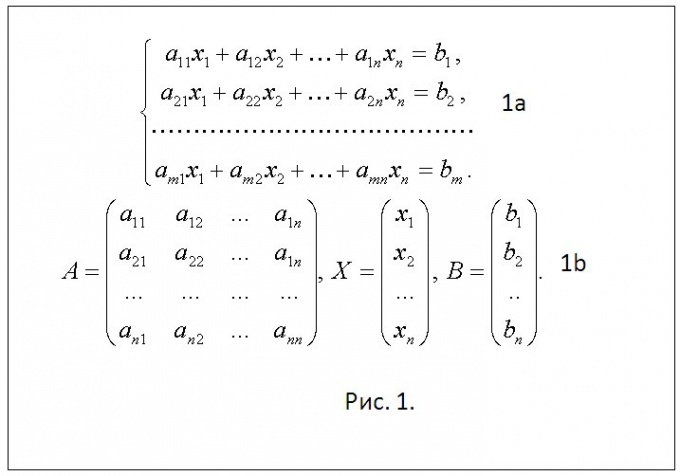
Начните процесс обучения с изучения способов решения системы двух линейных уравнений с двумя неизвестными X и Y методом исключения. a11*X+a12*Y=b1 (1); a21*X+a22*Y=b2 (2). Коэффициенты уравнений обозначены индексами, указывающими их месторасположения. Так коэффициент a21 подчеркивает тот факт, что он записан во втором уравнении на первом месте. В общепринятых обозначениях система записывается уравнениями расположенными друг под другом совместно обозначаемых фигурной скобкой справа или слева (подробнее см. рис. 1а).
2
Нумерация уравнений произвольна. Выберите из них самое простое, например то, в котором перед одной из переменных стоит коэффициент 1 или по крайней мере целое число. Если это уравнение (1), то далее выразите, скажем, неизвестное Y через X (случай исключения Y). Для этого преобразуйте (1) к виду a12*Y=b1-a11*X (или a11*X=b1-a12*Y при исключении Х)), а затем Y=(b1-a11*X)/a12. Подставив последнее в уравнение (2) запишите a21*X+a22*(b1-a11*X)/a12=b2. Решите это уравнение относительно X.
a21*X+a22*b1/a12-a11*a22*X/a12=b2; (a21-a11*a22/a12)*X=b2-a22*b1/a12;
X=(a12* b2-a22*b1)/(a12*a21-a11*a22) или X=(a22* b1-a12*b2)/(a11*a22-a12*a21).
Воспользовавшись найденной связью между Y и Х, окончательно получите и второе неизвестное Y=(a11* b2-a21*b1)/(a11*a22-a12*a21).
a21*X+a22*b1/a12-a11*a22*X/a12=b2; (a21-a11*a22/a12)*X=b2-a22*b1/a12;
X=(a12* b2-a22*b1)/(a12*a21-a11*a22) или X=(a22* b1-a12*b2)/(a11*a22-a12*a21).
Воспользовавшись найденной связью между Y и Х, окончательно получите и второе неизвестное Y=(a11* b2-a21*b1)/(a11*a22-a12*a21).
3
Если бы система была задана с конкретными числовыми коэффициентами, то и выкладки были бы менее громоздки. Зато общее решение дает возможность рассмотреть тот факт, что знаменатели при найденных неизвестных совершено одинаковы. Да и у числителей просматриваются некоторые закономерности их построения. Если размерность системы уравнений была бы большей двух, то метод исключения приводил бы к весьма громоздким выкладкам. Чтобы их избежать, разработаны чисто алгоритмические способы решения. Самый простой из них алгоритм Крамера (формулы Крамера). Для их изучения следует узнать, что такое общая система уравнений из n уравнений.
4
Система n линейных алгебраических уравнений с n неизвестными имеет вид (см. рис. 1a). В ней аij – коэффициенты системы,
хj – неизвестные, bi – свободные члены (i=1, 2, ... , n; j=1, 2, ... , п). Компактно такую систему можно записывать в матричной форме АХ=B. Здесь А – матрица коэффициентов системы, Х – матрица-столбец неизвестных, B – матрица-столбец свободных членов (см. рис 1b). По методу Крамера каждое неизвестное xi =∆i/∆ (i=1,2…,n). Определитель ∆ матрицы коэффициентов называют главным, а ∆i вспомогательным. Для каждой неизвестной вспомогательный определитель находят с помощью замены i-го столбца главного определителя на столбец свободных членов. Подробно метод Крамера для случая систем второго и третьего порядка представлен на рис. 2.
хj – неизвестные, bi – свободные члены (i=1, 2, ... , n; j=1, 2, ... , п). Компактно такую систему можно записывать в матричной форме АХ=B. Здесь А – матрица коэффициентов системы, Х – матрица-столбец неизвестных, B – матрица-столбец свободных членов (см. рис 1b). По методу Крамера каждое неизвестное xi =∆i/∆ (i=1,2…,n). Определитель ∆ матрицы коэффициентов называют главным, а ∆i вспомогательным. Для каждой неизвестной вспомогательный определитель находят с помощью замены i-го столбца главного определителя на столбец свободных членов. Подробно метод Крамера для случая систем второго и третьего порядка представлен на рис. 2.
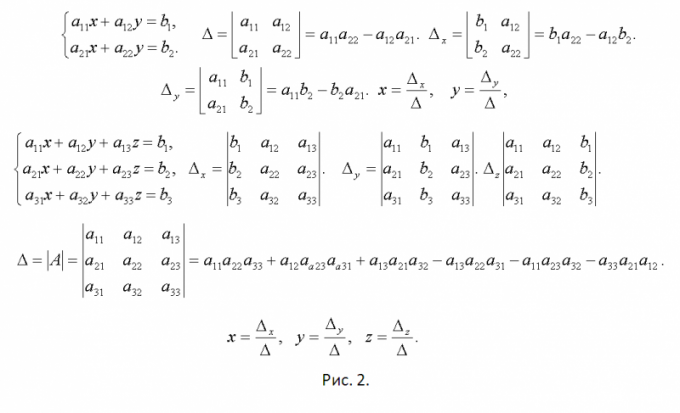
Видео по теме