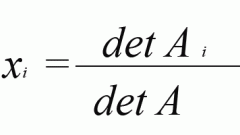Как разрешить систему линейных уравнений

Одной из основных задач математики является решение системы уравнений с несколькими неизвестными. Это очень практическая задача: есть несколько неизвестных параметров, на них накладывается несколько условий и требуется найти их наиболее оптимальную совокупность. Такие задачи являются обыденными в экономике, строительстве, проектировании сложных механических систем и вообще везде где требуется оптимизация затрат материальных и человеческих ресурсов. В связи с этим встает вопрос: а как же решать такие системы?

Инструкция

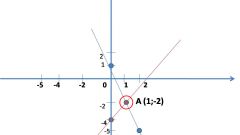
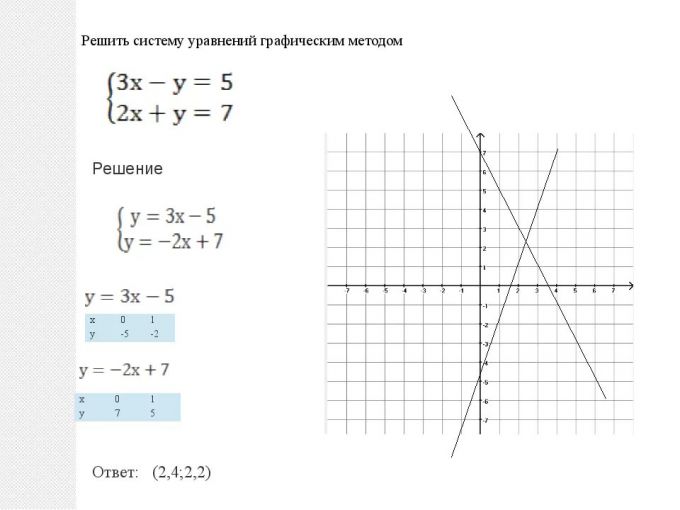
1. Математика дает нам два способа решения таких систем: графический и аналитический. Эти способы равнозначны, и нельзя сказать, что какой-то из них лучше или хуже. В каждой ситуации нужно в ходе оптимизации решения выбирать какой способ дает более простое решение. Но есть и некоторые типичные ситуации. Так, систему плоских уравнений, т. е. когда два графика имеют вид y=ax+b, проще решать графическим способом. Делается все очень просто: строятся две прямые: графики линейных функций, затем находится их точка пересечения. Координаты этой точки (абсцисса и ордината) и будут решением данного уравнения. Заметим также, что две прямые могут быть и параллельными. Тогда система уравнений не имеет решения, а функции называются линейно зависимыми.
   
2. Может случиться и обратная ситуация. Если нам нужно найти третью неизвестную, при двух линейно независимых уравнениях, тогда система будет недоопределена и иметь бесчисленное множество решений. В теории линейной алгебры доказывается, что система имеет единственное решение, тогда и только тогда, когда число уравнений совпадает с числом неизвестных.
3. Когда речь идет о трехмерном пространстве, т. е. когда графики функций имеют вид z=ax+by+c, графический метод становится трудно применимым, потому что появляется третье измерение, которое в разы усложняет поиск точки пересечения графиков. Тогда в математике прибегают к аналитическому или матричному методу. В теории линейной алгебры, они подробно описываются, а их суть заключена в следующем: преобразовать аналитические расчеты в операции сложения, вычитания и умножения, чтобы с ними справились вычислительные машины.
4. Метод оказался универсален для любой системы уравнений. В настоящее время даже ПК способен найти решение системы уравнений со 100 неизвестными! Использование матричных методов позволяет оптимизировать сложнейшие производственные процессы, что повышает качество продукции, которую мы потребляем.